
 +
+ =1,(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F,且它的长轴端点A及短轴端点B的连线AB平行于FM,求椭圆的离心率.
=1,(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F,且它的长轴端点A及短轴端点B的连线AB平行于FM,求椭圆的离心率.
 …(*)设点M(-c,y1),代入椭圆方程
…(*)设点M(-c,y1),代入椭圆方程 +
+ =1,
=1, +
+ =1,解之得y1=
=1,解之得y1= (舍负),所以MF1=
(舍负),所以MF1= ,
, ,
, ,可得e=
,可得e= (舍负)
(舍负) .
. .再根据点M在椭圆上,求出M的纵坐标,得出MF1=
.再根据点M在椭圆上,求出M的纵坐标,得出MF1= ,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e.
,再结合AO=a,BO=b,OF1=c,代入所得比例式,化简可得b=c,从而求出椭圆的离心率e.

科目:高中数学 来源: 题型:

(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,F2是右焦点,F1是左焦点,求∠F1QF2的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:选择题
从椭圆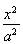 +
+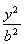 =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
(A) 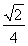 (B)
(B) 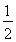 (C)
(C) 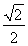 (D)
(D) 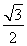
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求椭圆的离心率e;
(2)设Q为椭圆上任一点,F2为右焦点,求∠F1QF2的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省葫芦岛二中高二(上)12月月考数学试卷(文科)(解析版) 题型:解答题
 +
+ =1,(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F,且它的长轴端点A及短轴端点B的连线AB平行于FM,求椭圆的离心率.
=1,(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F,且它的长轴端点A及短轴端点B的连线AB平行于FM,求椭圆的离心率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com