定义在R上的函数y=f(x),且f(0)≠0,当x>0时,f(x)>1,且对任意a,b∈R,f(a+b)=f(a)f(b). 下列说法正确的是______(只填序号).
(1)f(0)=1;
(2)对任意x∈R,有f(x)>0;
(3)f(x)在R上是增函数;
(4)f(x)是R上的减函数.
解:(1)令a=b=0,则f(0+0)=f(0)f(0),即f(0)=[f(0)]
2,
又f(0)≠0,所以f(0)=1,故(1)正确;
(2)设x<0,则-x>0,所以f(-x)>1,
则f(x-x)=f(x)f(-x),即f(0)=f(x)f(-x),
所以f(x)=
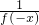
,
又f(-x)>1,所以0<f(x)<1,
因为x>0时,f(x)>1,f(0)=1,
所以对任意x∈R,有f(x)>0,故(2)正确;
(3)设x
1<x
2,
则f(x
1)-f(x
2)=f(x
1)-f[x
1+(x
2-x
1)]
=f(x
1)-f(x
1)f(x
2-x
1)=f(x
1)[1-f(x
2-x
1)],
由(2)知,f(x
1)>0,
由x
1<x
2,得x
2-x
1>0,所以f(x
2-x
1)>1,
所以1-f(x
2-x
1)<0,
所以f(x
1)-f(x
2)<0,即f(x
1)<f(x
2),
故f(x)为R上的增函数,故(3)正确;
由(3)知,(4)错误;
故答案为:(1)(2)(3).
分析:(1)令a=b=0,代入f(a+b)=f(a)f(b)即可求得;
(2)只需证明x<0时f(x)>0,令a=x,b=-x,代入f(a+b)=f(a)f(b)可得f(x)=
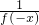
,由f(-x)范围可得f(x)范围;
(3)定义法:设x
1<x
2,作差f(x
1)-f(x
2)=f(x
1)-f[x
1+(x
2-x
1)],利用已知进行变形,由已知易判断差的符号;
点评:本题考查函数奇偶性的判断、单调性的证明,属中档题,抽象函数的单调性、奇偶性往往运用定义解决.

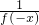 ,
,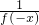 ,由f(-x)范围可得f(x)范围;
,由f(-x)范围可得f(x)范围;
