证明:(1)(2)①n=1时,a
1=

,
由于条件

,
∴a
2=sin(

a
1)=sin

=

.
∴0<a
1<a
2<1,故结论成立.
②假设n=k时结论成立,
即0<a
k<a
k+1<1,
则0<

a
k<

a
k+1<

.
∴0<sin(

a
k)<sin(

a
k+1)<1,
即0<a
k+1<a
k+2<1,
也就是说n=k+1时,结论也成立.
由①②可知,对一切n∈N
*均有0<a
n<a
n+1<1.
(3)∵1<1+a
n-1<2,
∴

<

(1+a
n-1)<

,
又a
n<a
n+1,
∴1+a
n-1≥1+a
1,(n≥2)
∴

(1+a
n-1)≥

(1+a
1)=

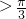
,
∴1-a
n=sin

-sin(

a
n-1)=2cos[

(1+a
n-1)]sin[

(1-a
n-1)]<sin[

(1-a
n-1)]
∵0<[

(1-a
n-1)]<

,又θ是锐角时,sinθ<θ,
∴sin[

(1-a
n-1)]<

(1-a
n-1)
∴

.(n≥2).
分析:(1)、(2)前两小问可一起进行证明.先看当n=1时,可求得a
2,则可验证结论成立;假设n=k时结论成立,根据0<a
k<a
k+1<1,推断出0<

a
k<

a
k+1<

.进而可知0<sin(

a
k)<sin(

a
k+1)<1,即0<a
k+1<a
k+2<1,结论成立,最后综合可知(1)(2)成立.
(3)由于1<1+a
n-1<2,结合(1)(2)中的结论得出

(1+a
1)的取值范围,从而1-a
n=sin

-sin(

a
n-1)=2cos[

(1+a
n-1)]sin[

(1-a
n-1)]<sin[

(1-a
n-1)],根据0<[

(1-a
n-1)]<

,结合三角函数的性质sinθ<θ即可证得结论.
点评:本题主要考查了数列递推式、数列与不等式的综合、不等式证明等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

 ,
, ,n∈N*.
,n∈N*. .(n≥2)
.(n≥2) )
) ,
, ,
, a1)=sin
a1)=sin  =
= .
. ak<
ak< ak+1<
ak+1< .
. ak)<sin(
ak)<sin(  ak+1)<1,
ak+1)<1, <
< (1+a n-1)<
(1+a n-1)< ,
, (1+a n-1)≥
(1+a n-1)≥ (1+a1)=
(1+a1)=
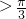 ,
, -sin(
-sin( a n-1)=2cos[
a n-1)=2cos[ (1+a n-1)]sin[
(1+a n-1)]sin[ (1-a n-1)]<sin[
(1-a n-1)]<sin[ (1-a n-1)]
(1-a n-1)] (1-a n-1)]<
(1-a n-1)]< ,又θ是锐角时,sinθ<θ,
,又θ是锐角时,sinθ<θ, (1-a n-1)]<
(1-a n-1)]< (1-a n-1)
(1-a n-1) .(n≥2).
.(n≥2). ak<
ak< ak+1<
ak+1< .进而可知0<sin(
.进而可知0<sin(  ak)<sin(
ak)<sin(  ak+1)<1,即0<ak+1<ak+2<1,结论成立,最后综合可知(1)(2)成立.
ak+1)<1,即0<ak+1<ak+2<1,结论成立,最后综合可知(1)(2)成立. (1+a1)的取值范围,从而1-a n=sin
(1+a1)的取值范围,从而1-a n=sin -sin(
-sin( a n-1)=2cos[
a n-1)=2cos[ (1+a n-1)]sin[
(1+a n-1)]sin[ (1-a n-1)]<sin[
(1-a n-1)]<sin[ (1-a n-1)],根据0<[
(1-a n-1)],根据0<[ (1-a n-1)]<
(1-a n-1)]< ,结合三角函数的性质sinθ<θ即可证得结论.
,结合三角函数的性质sinθ<θ即可证得结论.

 名校课堂系列答案
名校课堂系列答案