Question

已知双曲线x²-y²=1，过右焦点F₂的直线与右支交于A、B两点，且线段AF₂、BF₂的长度分别为m、n.

(1)求证：m·n≥1；

(2)若m＞n，当直线AB的斜率k∈［,3］时，求的取值范围.

Answer 1

答案：(1)证明：设双曲线的右准线为l，当AB垂直x轴时，A、B两点纵坐标分别是1，-1，

此时m·n=1符合条件.                                                         

当AB不垂直x轴时，不妨令m＞n.

作AP⊥l于P，BQ⊥l于Q，BK⊥AP于K,

M为BK与x轴交点(如下图).

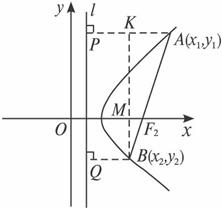
由双曲线的定义：|AP|=m，|BQ|=n,

又F₂到l的距离d=，

由直角三角形相似性质得：，

即.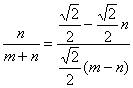

化简得2m·n=m+n≥,

∴m·n≥1.∵m≠n,∴m·n＞1成立,综上得m·n≥1.                                   

(2)解：F₂的坐标为(，0)，设AB的方程为x=ty+,

代入x²-y²=1,得(t²-1)y²+ty+1=0.设A(x₁,y₁),B(x₂,y₂).

由韦达定理：y₁+y₂=,y₁·y₂=，令=λ,则λ＞1,从而有y₁=-λy₂.

∴

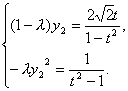
消去y₂得,

从而λ+-6，由k∈[，3]得t²=∈［］,∴3≤λ+≤4.

∵λ＞1,∴λ∈［］.