练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某校高一年级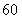名学生参加数学竞赛，成绩全部在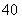分至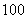分之间，现将成绩分成以下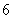段：

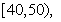
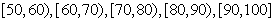    ，据此绘制了如图所示的频率分布直方图.

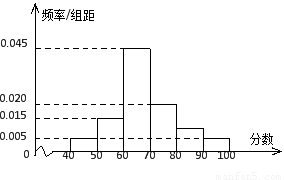
    （1）求成绩在区间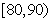的频率；

    （2）从成绩大于等于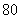分的学生中随机选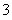名学生，其中成绩在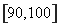内的学生人数为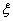，求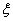的分布列与均值.

     

    【答案】

    （1）；（2）.

    【解析】

    试题分析：（1）根据频率分布直方图可知成绩在区间的频率为；（2）由已知和（1）的结果可知成绩在区间内的学生有人，成绩在区间内的学生有人，那么的所有可能取值为，然后求出所对应的概率分别为：

    ，列出分布列后求出的数学期望为：=

    试题解析：（1）根据频率分布直方图可知成绩在区间的频率为；

    （2）由已知和（1）的结果可知成绩在区间内的学生有人，成绩在区间内的学生有人， 依题意，可能取的值为.

    则：

    所以的分布列为：

    0

    1

    2

    3

    P

    则均值=

    考点：频率分布直方图，离散型随机变量的分布列与数学期望.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网某校高一年级共有学生320人．为调查高一年级学生每天晚自习自主支配学习时间（指除了完成教师布置的作业后学生根据自己的需要进行学习的时间）情况，学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查．根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据（单位：分钟），按照以下区间分为七组：①[0，10），②[10，20），③[20，30），④[30，40），⑤[40，50），⑥[50，60），⑦[60，70），得到频率分布直方图如图．已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人．
    （Ⅰ）求n的值；
    （Ⅱ）若高一全体学生平均每天晚自习自主支配学习时间少于45分钟，则学校需要减少作业量．根据以上抽样调查数据，学校是否需要减少作业量？（注：统计方法中，同一组数据常用该组区间的中点值作为代表）
    （Ⅲ）问卷调查完成后，学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈，了解各学科的作业布置情况，并从这7人中随机抽取两名学生聘为学情调查联系人，设第3组中学生被聘的人数是X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•资阳三模）对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，恨据此数据作出了右图所示的频数与频率的统计表和频率分布直方图：
    分组 频数 频率
    [10，15） 6 0.3
    [15，20） 8 N
    [20，25） M P
    [25，30） 2 0.1
    合计 M 1
    （I）求出表中M、p及图中a的值；
    （II）学校诀定对参加社区服务的学生进行表彰，对参加活动次数在[25，30]区间的每个学生发放价值80元的学习用品，对参加活动次数在[15，20）区间的每个学生发放价值40元的学习用品，对参加活动次数在[10，15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，设X为此二人所获得学习用品价值之差的绝对值，求X的分布列与数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•资阳三模）对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，恨据此数据作出了如图所示的频数与频率的统计表和频率分布直方图：
    分组 频数 频率
    [10，15） 6 0.3
    [15，20） 8 n
    [20，25） m p
    [25，30） 2 0.1
    合计 M 1
    （I）求出表中M、p及图中a的值；
    （II）学校诀定对参加社区服务的学生进行表彰，对参加活动次数在[25，30）区间的每个学生发放价值80元的学习用品，对参加活动次数在[20，25）区间的每个学生发放价值60元的学习用品，对参加活动次数在[15，20）区间的每个学生发放价值40元的学习用品，对参加活动次数在[10，15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，求此二人所获得学习用品价值之差的绝对值不超过20元的概率．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省漳州市四地七校高三第四次联考理科数学试卷（解析版） 题型：解答题

    （本小题满分13分）对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图：

    （I）求出表中M、p及图中a的值

    （II）学校决定对参加社区服务的学生进行表彰，对参加活动次数在［25，30］区间的每个学生发放价值80元的学习用品，对参加活动次数在［20,25）区间的每个学生发放价值60元的学习用品，对参加活动次数在［15,20）区间的每个学生发放价值40元的学习用品，对参加活动次数在［10,15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，设X为此二人所获得学习用品价值之差的绝对值，求X的分布列与数学期望E（X）。

     

    查看答案和解析>>

    同步练习册答案