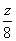练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图中阴影部分的点满足不等式组在这些点中，求使z=6x+8y取得最大值的点的坐标.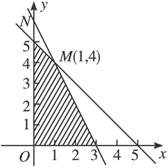

    解法一：由题图可知，使目标函数z=6x+8y取得最大值的点一定在边界x+y=5或2x+y=6上取得.

    ①当0≤x≤1时，z=6x+8y=6x+8(5-x)=40-2x在［0，1］上为减函数，所以当x=0时，zmax=40；

    ②当1≤x≤3时，z=6x+8(6-2x)=40-10x在［1，3］上也是减函数，所以当x=1时，zmax=38.

    由①②可知：当x=0时，z=6x+8y最大，此时y=5，所以所求的点的坐标为（0，5）.

    解法二：要使目标函数z=6x+8y取得最大值，即使y=-x+的截距最大，且阴影部分至少有一个在直线y=-x+上，因为-＞-1＞-2，所以易得知所求点的坐标为（0，5）.

    解法三：利用线性规划，按教材给出方法求解.

    作直线l：6x+8y=0，即作直线l：3x+4y=0.把直线l向右上方平移至l1的位置时，直线经过可行域上的N点时，z=6x+8y取最大值.

    解方程组得N点坐标为（0，5），代入目标函数z=6x+8y，z=?6×0+8×5=40.

    故知所求点为（0，5）时，z=6x+8y取最大值40.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （文科）图中阴影部分的点满足不等式组
    x+y≤6
    2x+y≤8
    x≥0，y≥0.
    在这些点中，使目标函数K=6x+8y取得最大值的点的坐标是
    （0，6）
    （0，6）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2000•上海）图中阴影部分的点满足不等式组
    x+y≤5
    2x+y≤6
    x≥0，y≥0
    ，在这些点中，使目标函数k=6x+8y取得最大值的点的坐标是
    （0，5）
    （0，5）
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    （文科）图中阴影部分的点满足不等式组
    x+y≤6
    2x+y≤8
    x≥0，y≥0.
    在这些点中，使目标函数K=6x+8y取得最大值的点的坐标是______．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年吉林省长春外国语学校高二（上）第二次月考数学试卷（解析版） 题型：填空题

    （文科）图中阴影部分的点满足不等式组在这些点中，使目标函数K=6x+8y取得最大值的点的坐标是    ．

    查看答案和解析>>

    同步练习册答案