分析:(Ⅰ)由cosA和cosB的值都大于0,得到A和B都为锐角,利用同角三角函数间的基本关系分别求出sinA和sinB的值,由A+B+C=π,得到C=π-(A+B),表示出cosC,代换后,利用诱导公式及两角和的余弦函数公式化简,再把各自的值代入即可求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;
(Ⅱ)由AB,sinA及sinB的值,利用正弦定理求出AC的值,最后利用锐角三角函数的定义,在直角三角形中,表示出sinA等于AB边上的高比上AC,即可得到高等于ACsinA,即可求出高的值.
解答:解:(Ⅰ)由
cosA=,
cosB=,得
A、B∈(0,),
所以
sinA=,sinB=.(3分)
因为
cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=,(6分)
且0<C<π,故
C=.(7分)
(Ⅱ)∵AB=
,sinC=
,sinB=
,
根据正弦定理得
=⇒AC===
,(10分)
所以AB边上的高为
AC•sinA=.(12分)
点评:此题考查了同角三角函数的基本关系,正弦定理,诱导公式及两角和与差的余弦函数公式,熟练掌握定理及公式是解本题的关键,做题时注意角度的范围.



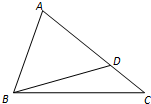 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=