Question

设关于x的方程4^x+（a-2）·2^x+a²=0有两个相异的正根，求实数a的取值范围.

Answer 1

思路分析：原方程可看成关于2^x的“二次”方程，利用二次方程根的知识解决.

解：方法一：令t=2^x，原方程化为t²+（a-2）t+a²=0,                             ①

∵原方程有两个相异正根，

∴关于t方程①有两个大于1的相异根.令f（t）=t²+（a-2）t+a²，考查f（t）的图象,如下图.

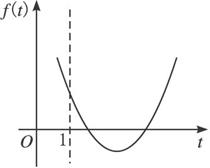
当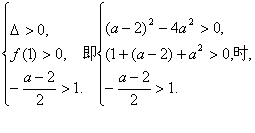

关于t的方程①有两个大于1的相异根，解得-2＜a＜.

∴a的取值范围为{a|-2＜a＜}.

方法二:令t=2^x，原方程化为

t²+（a-2）t+a²=0,               ①

∵原方程有两个相异正根，

∴关于t的方程①有两个大于1的相异根,设为t₁，t₂,

∵t₁＞1，t₂＞1,

∴t₁-1＞0,t₂-1＞0.

∴(t₁-1)+(t₂-1)=t₁+t₂-2=-(a-2)-2=-a＞0,

(t₁-1)·（t₂-1）=t₁·t₂-（t₁+t₂）+1=a²+a-2+1＞0.

∴方程①有两个大于1的相异正根的充要条件为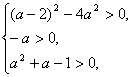

解得-2＜a＜.

∴a的取值范围为{a|-2＜a＜}.