练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，菱形ABCD所在平面与矩形ACEF所在平面相互垂直，点M是线段EF的中点。（1）求证：AM // 平面BDE（6分）  （2）当为何值时，平面DEF平面BEF？并证明你的结论。（8分）

    (Ⅰ) 略   (Ⅱ) …


    解析:

    证明（1）取AC与BD的交点N，连接EN， 1分

    由题意知：EN // AM，      4分又EN在平面BDE内，  …5分

    所以AM // 平面BDE   ……6分

    （2）当时，平面DEF平面BEF……7分

    因为面ACEF面ABCD，四边形ACEF为矩形，

    所以FA、EC都垂直于面ABCD，又四边形ABCD是菱形，

    所以FADECA，所以DF＝DE又M为EF的中点，所以DMEF，………10分

    当DMBM时，就有DM平面BEF  …12分

    即DMB＝90时，平面DEF平面BEF ∴……14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

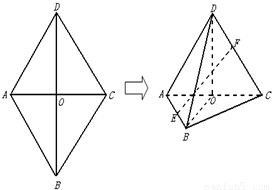
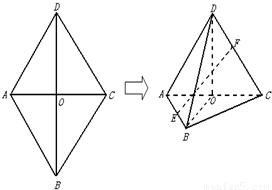
    （2012•闸北区二模）如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．
    （1）求线段EF的最大值与最小值；
    （2）当线段EF的长最小时，求异面直线AC与EF所成角θ的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

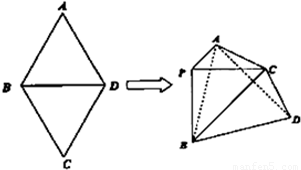
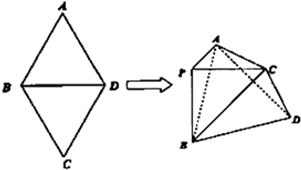    如图，菱形ABCD中，∠A=60°，把菱形ABCD沿对角线BD折成二面角A-BD-C，AC=BD，空间中的点P满足PA、PB、PC两两垂直，则下列命题中错误的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012年云南省昆明市高三复习适应性检测数学试卷（理科）（解析版） 题型：选择题

    如图，菱形ABCD中，∠A=60°，把菱形ABCD沿对角线BD折成二面角A-BD-C，AC=BD，空间中的点P满足PA、PB、PC两两垂直，则下列命题中错误的是（ ）

    A．二面角A-BD-C的余弦值为
    B．PC∥平面ABD
    C．PB与CD所成角为45°
    D．PB⊥BD

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市高考数学压轴试卷（理科）（解析版） 题型：解答题

    如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．
    （1）求线段EF的最大值与最小值；
    （2）当线段EF的长最小时，求异面直线AC与EF所成角θ的大小．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市闸北区高考数学二模试卷（理科）（解析版） 题型：解答题

    如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．
    （1）求线段EF的最大值与最小值；
    （2）当线段EF的长最小时，求异面直线AC与EF所成角θ的大小．

    查看答案和解析>>

    同步练习册答案