
 =(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)
=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)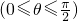 .
. ,且
,且 为坐标原点),求向量
为坐标原点),求向量 ;
; 与向量
与向量 共线,当k>4,且tsinθ取最大值4时,求
共线,当k>4,且tsinθ取最大值4时,求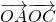 .
.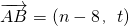 ,
,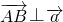 ,
, ,
, ,又
,又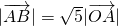 ,
, .
. 或
或 .
. 与向量
与向量 共线,
共线, .
. ,
,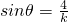 时,tsinθ取最大值
时,tsinθ取最大值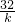 ,有
,有 ,得k=8.
,得k=8. ,k=8,tsinθ=4,得t=8,则
,k=8,tsinθ=4,得t=8,则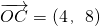 .
.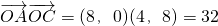 .
.

 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
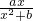 在x=1处取得极值2.
在x=1处取得极值2.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
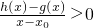 在D内恒成立,则称P为函数y=h(x)的“类对称点”,请你探究当a=4时,函数y=f(x)是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
在D内恒成立,则称P为函数y=h(x)的“类对称点”,请你探究当a=4时,函数y=f(x)是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 我校将在12月份举办艺术节,在艺术节初赛中,七位评委为某班的小品打出的分数如右图茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和标准差分别为
我校将在12月份举办艺术节,在艺术节初赛中,七位评委为某班的小品打出的分数如右图茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和标准差分别为



查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com