
如图在正方形ABCD-A1B1C1D1中,其棱长为1.
(1)求证:平面AB1C∥平面A1C1D;
(2)求:平面AB1C与平面A1C1D间的距离.

|
思路 在解答问题中要注意利用正方体中的线线平行、面面平行、线面垂直关系. 解答 (1)证法一 平面AB1C∥平面A1C1D 本证法是从线线平行关系出发得证的. 证法二 易知AA1和CC1确定一个平面AC1,于是, 本证法是从面面平行关系出发得证的. 证法三 连结BD1,BD 本证法是从线面垂直关系出发得证的,它的优点在于找到了两平行平面的一条公垂线,为解决下一问即计算两个平面之间的距离创造了条件. (2)设BD1∩平面AB1C=E, BD1∩平面A1C1D=F,BD∩AC=O, 由(1)证法三可知,线段EF的长就是这两个平行平面的距离,连EO、DF, ∴OE∥DF,E是BF的中点,得BE=EF, 同理,D1F=FE,∴EF= ∵BD1= 平面AB1C与平面A1C1D的距离为 评析 求二平行平面之间距离,还可以利用体积法来解. |


科目:高中数学 来源: 题型:
 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
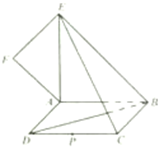 如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.查看答案和解析>>
科目:高中数学 来源: 题型:

A.AG⊥平面EFG B.AH⊥平面EFG
C.GF⊥平面AEF D.GH⊥平面AEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com