练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    图2-5-3所示是并列的三个大小相同的正方形,求证:∠1+∠2+∠3=90°.

    图2-5-3

    证明：以O为坐标原点,OC、OG所在的直线为x、y轴建系如上图,设正方形边长为1,则=(3,1),=(2,1),作向量=(3,-1),则与的夹角等于∠2+∠3.

    ∵||=5,| |=10, ·=2×3+1×(-1)=5,

    ∴cos〈,〉=.

    ∵〈,〉∈［0°,180°］,

    ∴〈,〉=45°,即∠2+∠3=45°.

    ∵∠1=45°,∴∠1+∠2+∠3=90°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
    （1）求出第4组的频率，并补全频率分布直方图；
    （2）根据样本频率分布直方图估计样本的中位数；
    （3）如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
    （1）求出第4组的频率，并补全频率分布直方图；
    （2）如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？
    （3）若该校决定在第4，5 组中随机抽取2名学生接受考官A的面试，第5组中有ξ名学生被考官A面试，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

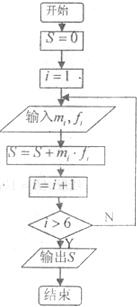    “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”．为提高公众对健康睡眠的科学认识和自我管理能力，某网站于3月13日起进行了为期一周的在线调查，共有200人参与．现将数据整理分组如表所示．
    （1）画出频率分布直方图；
    （2）调查对象中睡眠时间少于8的频率是多少？
    （3）为了对数据进行分析，采用了计算机辅助计算，算法流程如图所示．求输出的S的值，并说明S的统计意义．
    序号i 分组睡眠时间（小时） 组中值（m1） 频数（人数） 频率（f1）
    1 [4，5） 4.5 8 0.04
    2 [5，6） 5.5 52 0.26
    3 [6，7） 6.5 60 0.30
    4 [7，8） 7.5 56 0.28
    5 [8，9） 8.5 20 0.10
    6 [9，10） 9.5 4 0.02

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图所示是一个11阶杨辉三角：

    （1）求第20行中从左到右的第4个数；
    （2）若第n行中从左到右第14与第15个数的比为
    23
    ，求n的值；
    （3）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m，k（m，k∈N*）的数学公式表示上述结论，并给予证明．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    2008年北京奥运会中国跳水梦之队取得了辉煌的成绩．据科学测算，跳水运动员进行10米跳台跳水训练时，身体(看成一点)在空中的运动轨迹(如下图所示)是一条经过坐标原点的抛物线(图中标出数字为已知条件)，且在跳某个规定的翻腾动作时，正常情况下运动员在空中的最高点距水面米，入水处距池边4米，同时运动员在距水面5米或5米以上时，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误．
    (1)求这个抛物线的解析式；
    (2)在某次试跳中，测得运动员在空中的运动轨迹为(1)中的抛物线，且运动员在空中调整好入水姿势时距池边的水平距离为米，问此次跳水会不会失误？请通过计算说明理由；
    (3)某运动员按(1)中抛物线运行，要使得此次跳水成功，他在空中调整好入水姿势时，距池边的水平距离至多应为多大？

    查看答案和解析>>

    同步练习册答案