
(1)求椭圆C的方程;
(2)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A、B两点,且A、B关于点M对称,求直线l的方程.
解法一:(1)因为点P在椭圆C上,所以2a=|PF1|+|PF2|=6,a=3.
在Rt△PF1F2中,|F1F2|=![]() =2
=2![]() ,故椭圆的半焦距c=
,故椭圆的半焦距c=![]() ,
,
从而b2=a2-c2=4,所以椭圆C的方程为![]() =1.
=1.
(2)设A、B的坐标分别为(x1,y1),(x2,y2).
已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1),
从而可设直线l的方程为y=k(x+2)+1,
代入椭圆C的方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A、B关于点M对称,所以![]() =
=![]() =-2,解得k=
=-2,解得k=![]() .
.
所以直线l的方程为y=![]() (x+2)+1,即8x-9y+25=0.
(x+2)+1,即8x-9y+25=0.
(经检验,所求直线方程符合题意)
解法二:(1)同解法一.(2)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A、B的坐标分别为(x1,y1)、(x2,y2).由题意x1≠x2且![]() =1,①
=1,①
![]() =1.②
=1.②
由①-②,得![]() =0.③
=0.③
因为A、B关于点M对称,所以x1+x2=-4,y1+y2=2.代入③得![]() ,即直线l的斜率为
,即直线l的斜率为![]() ,
,
所以直线l的方程为y-1=![]() (x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意).
(x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意).


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
已知椭圆C: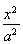 +
+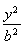 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为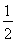 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+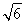 =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)求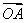 ·
·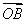 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
设椭圆C: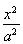 +
+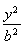 =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为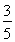 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为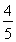 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
已知椭圆C: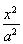 +
+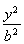 =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P(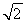 ,
,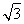 ).
).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,2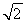 ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:填空题
已知F1、F2是椭圆C: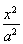 +
+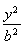 =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且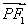 ⊥
⊥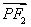 ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com