


 =0.1,P(X1=9)=
=0.1,P(X1=9)=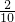 =0.2,
=0.2,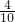 =0.4.
=0.4.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| A、甲比乙好 | B、乙比甲好 | C、甲、乙一样好 | D、难以确定 |
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上期中文科数学试卷(解析版) 题型:选择题
设甲、乙两名射手各打了5发子弹,每发子弹击中环数如下:
甲:10, 6, 8, 7, 9
乙:8, 9, 9, 7, 7
根据已学的统计知识,从总体水平和稳定性两方面考虑,甲、乙两名射手的射击技术评定情况是( )
A.甲比乙好 B.乙比甲好 C.甲、乙一样好 D.难以确定
查看答案和解析>>
科目:高中数学 来源:山东模拟 题型:单选题
| A.甲比乙好 | B.乙比甲好 |
| C.甲、乙一样好 | D.难以确定 |
查看答案和解析>>
科目:高中数学 来源:山东模拟 题型:单选题
| A.甲比乙好 | B.乙比甲好 |
| C.甲、乙一样好 | D.难以确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com