练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数数学公式的定义域是[n，n+1]（n为自然数） 那么f（x）的值域中的整数个数是________．

    2n
    分析：f（x）的对称轴是x=，当n≥1时，f（x）在[n，n+1]上是单调递增的，因为f（n）和f（n+1）都不是整数，
    故f（x）的值域中的整数个数问题只要计算f（n+1）-f（n）即可；n=0时，值域为[f（），f（0）]．
    解答：当n≥1时，f（x）在[n，n+1]上是单调递增的，
    f（n+1）-f（n）=（n+1）2-（n+1）+-n2+n-=2n，故f（x）的值域中的整数个数是2n，
    n=0时，值域为[f（），f（0）]=[，]，无整数．
    故答案为：2n
    点评：本题考查二次函数的值域问题，对问题的化归转化能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若函数f(x)=x2-x+
    12
    的定义域是[n，n+1]（n为自然数） 那么f（x）的值域中的整数个数是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：重庆市重点中学高2007级高三第四次月考数学试题(理科)[原创]新人教 新人教 题型：022

    给出下列4个命题：

    ①函数f(x)＝x|x|＋ax＋m是奇函数的充要条件是m＝0：

    ②若函数的定义域是{x|x＜1}，则a＜－1；

    ③若，则(其中n∈N+)；

    ④圆：x2＋y2－10x＋4y－5＝0上任意点M关于直线ax－y－5a＝2的对称点，M′也在该圆上．填上所有正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省菏泽市东明一中高一（上）10月段考数学试卷（解析版） 题型：填空题

    关于下列命题：
    ①若函数y=x+1的定义域是{x|x≤0}，则它的值域是{y|y≤1}；
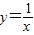    ②若函数的定义域是{x|x＞2}，则它的值域是；
    ③若函数y=x2的值域是{y|0≤y≤4}，则它的定义域不一定是{x|-2≤x≤2}；
    ④若函数y=x-2的值域是{y|y≤4，y∈N+}，则它的定义域是．
    其中不正确的命题的序号是    （ 注：把你认为不正确的命题的序号都填上）．

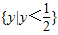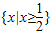    查看答案和解析>>

    科目：高中数学 来源：2010年高考数学专项复习：二次函数（解析版） 题型：解答题

    若函数的定义域是[n，n+1]（n为自然数） 那么f（x）的值域中的整数个数是    ．

    查看答案和解析>>

    同步练习册答案