
函数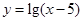 的的定义域是( )
的的定义域是( )
A.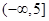 B.
B.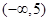 C.
C.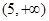 D.
D.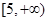
科目:高中数学 来源:2010-2011学年新疆乌鲁木齐市高三(上)期末数学试卷(解析版) 题型:选择题
 有无数个解;③函数{x}是周期函数;④函数{x}是增函数.其中正确的序号是( )
有无数个解;③函数{x}是周期函数;④函数{x}是增函数.其中正确的序号是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第一次月考文科数学试卷(解析版) 题型:填空题
设函数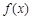 的定义域为
的定义域为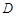 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称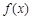 为
为 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题:
①函数 为
为 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考理科数学试卷(解析版) 题型:填空题
设函数 的定义域为
的定义域为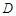 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题:
①函数 为
为 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考文科数学试卷(解析版) 题型:填空题
设函数 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数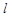 使得对于任意
使得对于任意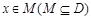 ,有
,有 ,且
,且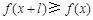 ,则称
,则称 为
为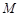 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题:
①函数 为
为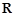 上的“1高调函数”;
上的“1高调函数”;
②函数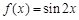 为
为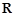 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是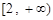 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省、临川一中高三8月联考文科数学试卷(解析版) 题型:填空题
设函数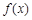 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数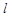 使得对于任意
使得对于任意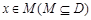 ,有
,有 ,且
,且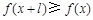 ,则称
,则称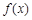 为
为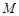 上的“
上的“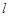 高调函数”.现给出下列命题:
高调函数”.现给出下列命题:
①函数 为
为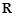 上的“1高调函数”;
上的“1高调函数”;
②函数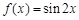 为
为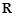 上的“
上的“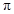 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“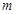 高调函数”,那么实数
高调函数”,那么实数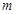 的取值范围是
的取值范围是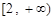 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com