已知集合A={x|x2-5x+4≤0},B={x|x2-2ax+a+2≤0},若B⊆A,求实数a的取值范围.
分析:设f(x)=x2-2ax+a+2,它的图象是一条开口向上的抛物线,B⊆A可知集合B为空集或解决是[1,4]的子区间,结合图象建立不等关系,解之即可.
解答: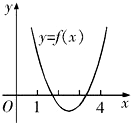
解:A={x|x
2-5x+4≤0}={x|1≤x≤4}.
设f(x)=x
2-2ax+a+2,它的图象是一条开口向上的抛物线
(1)若B=?,满足条件,此时△<0,即4a
2-4(a+2)<0,
解得-1<a<2;
(2)若B≠?,设抛物线与x轴交点的横坐标为x
1,x
2,
且x
1≤x
2,欲使B⊆A,应有{x|x
1≤x≤x
2}⊆{x|1≤x≤4},
结合二次函数的图象,得
即
| | 1-2a+a+2≥0 | | 42-8a+a+2≥0 | | 1≤a≤4 | | 4a2-4(a+2)≥0 |
| |
解得
2≤a≤.
综上可知a的取值范围是
(-1,].
点评:本题主要考查了集合的包含关系判断及应用,以及二次函数的图象,属于基础题.

 解:A={x|x2-5x+4≤0}={x|1≤x≤4}.
解:A={x|x2-5x+4≤0}={x|1≤x≤4}.
