练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在平面直角坐标系xOy中，过定点C(0,p)作直线与抛物线x2=2py(p＞0)相交于A、B两点.

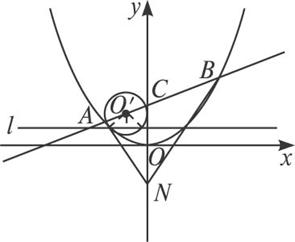
    （1）若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值.

    （2）是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得的弦长恒为定值？若存在，求出l的方程;若不存在，请说明理由.

    (1)依题意，点N的坐标为N(0,-p)，可设A(x1,y1)，B(x2,y2),

    直线AB的方程为y=kx+p，与x2=2py联立得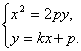

    消去y得x2-2pkx-2p2=0.

    由韦达定理得x1+x2=2pk,x1x2=-2p2.

    于是S△ABN=S△BCN+S△ACN=·2p|x1-x2|=p|x1-x2|

    =p=p=2p2,

    ∴当k=0时,(S△ABN)min=2p2.

    (2)假设满足条件的直线l存在，其方程为y=a，

    设AC的中点为O′，l与AC为直径的圆相交于点P，Q,PQ的中点为H，

    则O′H⊥PQ,Q′点的坐标为(,).

    ∵|O′P|=|AC|==,|O′H|=|a|=|2a-y1-p|,

    ∴|PH|2=|O′P|2-|O′H|2=(y12+p2)(2a-y1-p)2=(a)y1+a(p-a).

    ∴|PQ|2=(2|PH|)2=4［(a)y1+a(p-a)］.

    令a=0,得a=,此时|PQ|=p为定值,故满足条件的直线l存在,其方程为y=,即抛物线的通径所在的直线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
    		2
    的圆C经过坐标原点O，椭圆
    x2
    a2
    +
    y2
    9
    =1(a＞0)    与圆C的一个交点到椭圆两焦点的距离之和为10．
    （1）求圆C的方程；
    （2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
    3
    5
    ，点B的纵坐标是
    12
    13
    ，则sin（α+β）的值是
    16
    65
    16
    65
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，若焦点在x轴的椭圆
    x2
    m
    +
    y2
    3
    =1    的离心率为
    1
    2
    ，则m的值为
    4
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•泰州三模）选修4-4：坐标系与参数方程
    在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
    3t
    ，0)    ，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左焦点为F1（-1，0），且椭圆C的离心率e=
    1
    2
    ．
    （1）求椭圆C的方程；
    （2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
    （3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
    16
    7
    相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案