
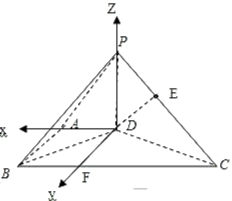
如图,在底面为直角梯形的四棱锥P﹣ABCD中,AD∥BC,∠ABC=90°,PD⊥面ABCD.
AD=1, ,BC=4.
,BC=4.
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成角;
(3)设点E在棱PC上, ,若DE∥面PAB,求λ的值.
,若DE∥面PAB,求λ的值.

解:(1)∵∠DAB=90°,AD=1,AB=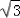 ,
,
∴BD=2,∠ABD=30°,
∵BC∥AD
∴∠DBC=60°,BC=4,
由余弦定理得DC=2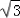 ,
,
BC2=DB2+DC2,∴BD⊥DC,
∵PD⊥面ABCD,∴BD⊥PD,PD∩CD=D,∴BD⊥面PDC,
∵PC在面PDC内,∴BD⊥PC
(2)在底面ABCD内过D作直线DF∥AB,交BC于F,分别以DA、DF、DP为x、y、z轴建立如图空间坐标系,
由(1)知BD⊥面PDC,∴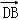 就是面PDC的法向量,
就是面PDC的法向量,
A(1,0,0),B(1,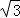 ,0),P(0,0,a)
,0),P(0,0,a)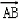 =(0,
=(0,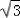 ,0),
,0),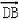 =(1,
=(1,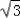 ,0),
,0),
设AB与面PDC所成角大小为θ,sinθ=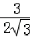 =
=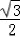 ,
,
∵θ∈(0,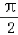 )∴θ=
)∴θ=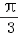
(3)在(2)中的空间坐标系中A(1,0,0),B(1,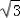 ,0),P(0,0,a),
,0),P(0,0,a),
C(﹣3,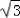 ,0),
,0),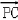 =(﹣3,
=(﹣3,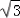 ,﹣a),
,﹣a),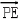 =(﹣3λ,
=(﹣3λ,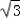 λ,﹣aλ),
λ,﹣aλ),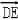 =
=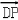 +
+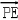 =(0,0,a)+(﹣3λ,
=(0,0,a)+(﹣3λ,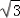 λ,﹣aλ)=(﹣3λ,
λ,﹣aλ)=(﹣3λ,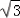 λ,a﹣aλ)
λ,a﹣aλ)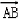 =(0,
=(0,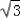 ,0),
,0),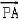 =(1,0,﹣a),
=(1,0,﹣a),
设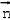 =(x,y,z)为面PAB的法向量,
=(x,y,z)为面PAB的法向量,
由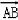
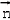 =0,得y=0,
=0,得y=0,
由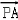
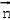 =0,得x﹣az=0,取x=a,z=1,
=0,得x﹣az=0,取x=a,z=1,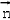 =(a,0,1),
=(a,0,1),
由DE∥面PAB得: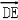 ⊥
⊥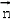 ,
,
∴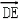
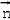 =0,﹣3aλ+a﹣aλ=0,∴λ=
=0,﹣3aλ+a﹣aλ=0,∴λ=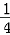


科目:高中数学 来源: 题型:
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年天津一中高三(下)第二次月考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省五市高三第一次联考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com