分析:以B1为坐标原点,建立空间坐标系,设正方体ABCD-A1B1C1D1的棱长为1,可求出各顶点的坐标
(1)分别求出AC与A1D方向向量,代入向量夹角公式,可得AC与A1D所成角的大小;
(2)要证明两个平面平行,由面面平行的判定定理知:须在某一平面内寻找两条相交且与另一平面平行的直线.求出AB1与C1D的方向向量,通过证明向量平行,得到AB1与C1D平行,同理证明出AD1与C1B平行,可得结论.
(3)求出A1C的方向向量,并证明A1C的方向向量是平面BDC1的法向量,可得A1C⊥平面BDC1.
解答:解:令正方体ABCD-A
1B
1C
1D
1的棱长为1,以B
1为坐标原点,建立空间坐标系如下图所示:
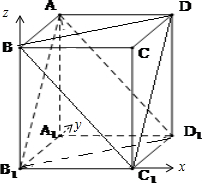
(1)则A(0,1,1),C(1,0,1),A
1(0,1,0),D(1,1,1)
∴
=(1,-1,0),
=(1,0,1)
设AC与A
1D所成角的大小为θ
则cosθ=
=
故θ=
证明:(2)∵
=
=(0,-1,-1)
∴AB
1∥C
1D,
又∵AB
1?平面AB
1D
1,C
1D?平面AB
1D
1,
∴C
1D∥平面AB
1D
1,
同理可证:C
1B∥平面AB
1D
1.
又C
1B∩C
1D=C
1,
∴平面AB
1D
1∥平面BDC
1.
(3)
=(1,-1,1),
=(1,1,0),
=(1,0,-1)
∴
•
=0,即
⊥
,即A
1C⊥BD
且
•
=0,即
⊥
,即A
1C⊥BC
1.
∵BD∩BC
1=B,BD,BC
1?平面BDC
1.
∴A
1C⊥平面BDC
1.
点评:第一问在使用传统方法证明时,必须强调一作二证三计算的步骤,第二问在证明线面平行时,一定要强调平面外和平面内的直线.

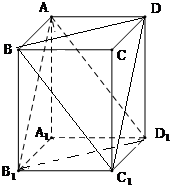 如图,在正方体ABCD-A1B1C1D1中,求证:
如图,在正方体ABCD-A1B1C1D1中,求证:


 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则