练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f（x）=数学公式+数学公式的定义域为________．

    （-1，1）∪（1，2]
    分析：本题考查的知识点是函数的定义域及其求法，根据函数的定义为使函数f（x）=+的解析式有意义的自变量x取值范围，我们可以构造关于自变量x的不等式，解不等式即可得到答案．
    解答：要使函数f（x）=+的解析式有意义，
    自变量x需满足
    解得：-1＜x＜1或1＜x≤2
    故答案为：（-1，1）∪（1，2]
    点评：求函数的定义域时要注意：（1）当函数是由解析式给出时，其定义域是使解析式有意义的自变量的取值集合．（2）当函数是由实际问题给出时，其定义域的确定不仅要考虑解析式有意义，还要有实际意义（如长度、面积必须大于零、人数必须为自然数等）．（3）若一函数解析式是由几个函数经四则运算得到的，则函数定义域应是同时使这几个函数有意义的不等式组的解集．若函数定义域为空集，则函数不存在．（4）对于（4）题要注意：①对在同一对应法则f 下的量“x”“x+a”“x-a”所要满足的范围是一样的；②函数g（x）中的自变量是x，所以求g（x）的定义域应求g（x）中的x的范围．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=ax-
    b
    x
    -2lnx，f(1)=0    ．
    （1）若函数f（x）在其定域义内为单调函数，求实数a的取值范围；
    （2）若函数f（x）的图象在x=1处的切线的斜率为0，且an+1=f′(
    1
    an+1
    )-nan+1    ．
    ①若a1≥3，求证：an≥n+2；
    ②若a1=4，试比较
    1
    1+a1
    +
    1
    1+a2
    +…+
    1
    1+an
    与
    2
    5
    的大小，并说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）若任意直线l过点F（0，1），且与函数f（x）=
    1
    4
    x2    的图象C交于两个不同的点A，B，分别过点A，B作C的切线，两切线交于点M，证明：点M的纵坐标是一个定值，并求出这个定值；
    （2）若不等式f（x）≥g（x）恒成立，g（x）=alnx（a＞o）求实数a的取值范围；
    （3）求证：
    ln24
    24
    +
    ln34
    34
    +
    ln44
    44
    +…
    lnn4
    n4
    ＜
    2
    e
    ，（其中e为无理数，约为2.71828）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数数学公式．
    （1）若函数f（x）在其定域义内为单调函数，求实数a的取值范围；
    （2）若函数f（x）的图象在x=1处的切线的斜率为0，且数学公式．
    ①若a1≥3，求证：an≥n+2；
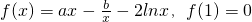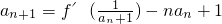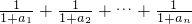    ②若a1=4，试比较数学公式与数学公式的大小，并说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数f(x)=ax-
    b
    x
    -2lnx，f(1)=0    ．
    （1）若函数f（x）在其定域义内为单调函数，求实数a的取值范围；
    （2）若函数f（x）的图象在x=1处的切线的斜率为0，且an+1=f′(
    1
    an+1
    )-nan+1    ．
    ①若a1≥3，求证：an≥n+2；
    ②若a1=4，试比较
    1
    1+a1
    +
    1
    1+a2
    +…+
    1
    1+an
    与
    2
    5
    的大小，并说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年四川省南充高中高三第六次月考数学试卷（理科）（解析版） 题型：解答题

    已知函数．
    （1）若函数f（x）在其定域义内为单调函数，求实数a的取值范围；
    （2）若函数f（x）的图象在x=1处的切线的斜率为0，且．
    ①若a1≥3，求证：an≥n+2；
    ②若a1=4，试比较与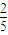的大小，并说明你的理由．

    查看答案和解析>>

    同步练习册答案