练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点P(t，y)在函数f(x)＝(x≠－1)的图象上，且有t2－c2at＋4c2＝0(c≠0)．

    求证：(1)|ac|≥4；

    (2)在(－1，＋∞)上f(x)单调递增．

    (3)f(|a|)＋f(|c|)＞1．

    答案：
    解析：

    　　证明：(1)∵t∈R，t≠－1，∴Δ＝(－c2a)2－16c2＝c4a2－16c2≥0，

    　　∵c≠0，∴c2a2≥16，∴|ac|≥4．

    　　(2)由f(x)＝1－，

    　　证法一：设－1＜x1＜x2，则f(x2)－f(x1)＝1－－1＋＋1＝．

    　　∵－1＜x1＜x2，

    　　∴x2－x1＞0，x1＋1＞0，x2＋1＞0．

    　　∴f(x2)－f(x1)＞0，即f(x2)＞f(x1)．

    　　∴x＞－1时，f(x)单调递增．

    　　证法二：由(x)＝，x≠－1，得(x)＞0．

    　　∴x＞－1时，f(x)单调递增．

    　　(3)∵f(x)在x＞－1时单调递增，|c|≥＞0．

    　　∴f(|c|)≥f()＝，

    　　f(|a|)＋f(|c|)≥＝1．

    　　∴f(|a|)＋f(|c|)＞1．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点P为圆x2+y2=4上的动点，且P不在x轴上，PD⊥x轴，垂足为D，线段PD中点Q的轨迹为曲线C，过定点M（t，0）（0＜t＜2）任作一条与y轴不垂直的直线l，它与曲线C交于A、B两点．
    （1）求曲线C的方程；
    （2）试证明：在x轴上存在定点N，使得∠ANB总能被x轴平分．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考北京四中全真模拟试卷——数学 题型：013

    已知点P(t，m)是函数y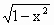＝图象上的动点，过点P作此函数图象的切线，切线斜率k是点P横坐标t的函数，记为k＝f(t)，则函数k＝f(t)在(－1，1)上是

    [　　]

    A．单调递增函数

    B．单调递减函数

    C．(－1，0]上增函数，在[0，1)上减函数．

    D．(－1，0]上减函数，在[0，1)上增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题满分14分)

    已知点P ( t , y )在函数f ( x ) = (x ?? –1)的图象上，且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).

    (1) 求证：| ac | ?? 4;(2) 求证：在(–1，+∞）上f ( x )单调递增.(3) (仅理科做)求证：f ( | a | ) + f ( | c | ) > 1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点P(t,y)在函数f(x)=(x≠-1)的图象上,且有t2-c2at+4c2=0(c≠0).

    求证:(1)|ac|≥4;

    (2)在(-1,+∞)上f(x)单调递增.

    (3)f(|a|)+f(|c|)>1.

    查看答案和解析>>

    同步练习册答案