求值:(log62)2+log63×log612.
解:原式=(log
62+log
63)log
62+log
63
=log
62+log
63=1.
∴(log
62)
2+log
63×log
612=1.
分析:先对后一项:log
63×log
612利用对数的运算法则进行化简得到:log
63+log
63×log
62,再和前面一项提取公因式log
62后利用对数的运算性质:log
a(MN)=log
aM+log
aN进行计算,最后再将前面计算的结果利用log
62+log
63=1进行运算.从而问题解决.
点评:本小题主要考查对数的运算性质、对数的运算性质的应用等基础知识,考查运算求解能力.属于基础题.对数的运算性质:log
a(MN)=log
aM+log
aN; log
a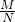
=log
aM-log
aN;log
aM
n=nlog
aM等.

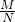 =logaM-logaN;logaMn=nlogaM等.
=logaM-logaN;logaMn=nlogaM等. 
