练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过点（1，0）的直线l与中心在原点，焦点在x轴上且离心率为的椭圆C相交于A、B两点，直线y=x过线段AB的中点，同时椭圆C上任一点与右焦点关于直线l对称，试求直线l与椭圆C的方程.

    解：由e==得,从而a2=2b2,c=b.

    设椭圆C的方程为x2+2y2=2b2,l的方程为y=k（x-1）,代入C方程,得（1+2k2）x2-4k2x+　2k2-2b2=0,

    则x1+x2=,y1+y2=k（x1-1）+k（x2-1）=k（x1+x2）-2k=-.

    直线y=x过AB的中点（,）,则=·,解得k=0或k=-1.

    若k=0,则l：y=0,焦点F（c,0）关于l的对称点就是F点本身,不能在椭圆C上,所以k=0舍去;若k=-1,l：y=-（x-1）,即y=-x+1,右焦点为（b,0）,其关于l的对称点设为（x′,y′）.

    则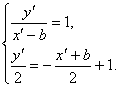解得

    点（1,1-b）在椭圆上，得1+2（1-b）2=2b2,?b2=,a2=.?

    ∴所求椭圆C的方程为：=1,l的方程为y′=-x+1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

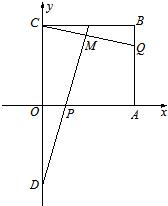    精英家教网如图所示，在直角坐标平面上的矩形OABC中，|OA|=2，| OC |=
    		3
    ，点P，Q满足
    OP
    =
    λOA
    ，
    AQ
    =( 1-λ )
    AB
      ( λ∈R )    ，点D是C关于原点的对称点，直线DP与CQ相交于点M．
    （Ⅰ）求点M的轨迹方程；
    （Ⅱ）若过点（1，0）的直线与点M的轨迹相交于E，F两点，求△AEF的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线M：y2=4x，圆N：（x-1）2+y2=r2（其中r为常数，r＞0）．过点（1，0）的直线l交圆N于C、D两点，交抛物线M于A、B两点，且满足|AC|=|BD|的直线l只有三条的必要条件是（　　）
    A、r∈（0，1]
    B、r∈（1，2]
    C、r∈(
    3
    2
    ，4)
    D、r∈[
    3
    2
    ，+∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的两个焦点F1(-
    		3
    ，0)，F2(
    		3
    ，0)    ，且椭圆短轴的两个端点与F2构成正三角形．
    （I）求椭圆的方程；
    （Ⅱ）若过点（1，0）的直线l与椭圆交于不同两点P、Q，试问在x轴上是否存在定点E（m，0），使
    PE
    •
    QE
    恒为定值？若存在，求出E的坐标及定值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在（0，+∞）上的函数f(x)=
    (4k-1)ln
    1
    x
    ，x∈(0 ， e]
    kx2-kx，x∈(e ， +∞)
    是增函数
    （1）求常数k的取值范围
    （2）过点（1，0）的直线与f（x）（x∈（e，+∞））的图象有交点，求该直线的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•泰安一模）已知椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的一个焦点与抛物线y2=4
    		3
    x    的焦点F重合，且椭圆短轴的两个端点与F构成正三角形．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）若过点（1，0）的直线l与椭圆交于不同两点P、Q，试问在x轴上是否存在定点E（m，0），使
    PE
    •
    QE
    恒为定值？若存在，求出E的坐标及定值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案