
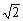
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
(18)本小题主要考查线面关系、二面角和函数极值等基础知识,考查空间想象能力和推理论证能力.
解:(Ⅰ)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形,∴MN=PQ.
由已知,
CM=BN=a,CB=AB=BE=1,
∴AC=BF=![]() ,
,
![]() =
=![]() ,
,![]() =
=![]() .
.
即CP=BQ=![]() .
.
∴MN=PQ=![]()
=![]()
=![]() (0<a<
(0<a<![]() ).
).
(Ⅱ)由(Ⅰ),
MN=![]() ,
,
所以,当a=![]() 时,MN=
时,MN=![]() .
.
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为![]() .
.
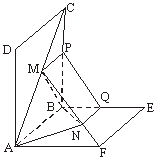
(Ⅲ)取MN的中点G,连结AG、BG,
∵AM=AN,BM=BN,G为MN的中点
∴AG⊥MN,BG⊥MN,∠AGB即为二面角α的平面角,
又AG=BG=![]() ,所以,由余弦定理有cosα=
,所以,由余弦定理有cosα=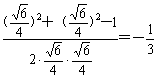 .
.
故所求二面角α=arccos(-![]() ).
).


科目:高中数学 来源: 题型:
 (2011•安徽模拟)古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )
(2011•安徽模拟)古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
如图,正方形 的边长为18,其内有一点P与
的边长为18,其内有一点P与 、
、 边的距离都是4,Q点与AB、
边的距离都是4,Q点与AB、 的距离都是2,将此正方形卷成一个圆柱形筒,使
的距离都是2,将此正方形卷成一个圆柱形筒,使 与AB重合,求P、Q两点间的距离.
与AB重合,求P、Q两点间的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,正方形
 的边长为18,其内有一点P与
的边长为18,其内有一点P与 、
、 边的距离都是4,Q点与AB、
边的距离都是4,Q点与AB、 的距离都是2,将此正方形卷成一个圆柱形筒,使
的距离都是2,将此正方形卷成一个圆柱形筒,使 与AB重合,求P、Q两点间的距离.
与AB重合,求P、Q两点间的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
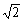
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com