
分析 由正四面体的棱长为1,所以此四面体一定可以放在棱长为$\frac{\sqrt{2}}{2}$的正方体中,由此能求出此四面体的体积.
解答 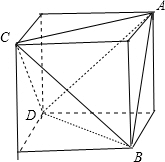 解:∵正四面体的棱长为,
解:∵正四面体的棱长为,
∴此四面体一定可以放在正方体中,
∴我们可以在正方体中寻找此四面体.
如图所示,四面体ABCD满足题意,BC=1,
∴正方体的棱长为$\frac{\sqrt{2}}{2}$,
∴此四面体的体积为($\frac{\sqrt{2}}{2}$)3-4×$\frac{1}{3}×\frac{1}{2}×$$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{12}$.
点评 本题考查四面体的体积问题,考查了空间想象能力,其解答的关键是在正方体中寻找此四面体.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
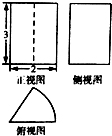 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )| A. | 2π | B. | π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.
圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com