已知数列{an}的前n项和Sn
(1)若Sn=3n+1,求通项公式an;
(2)若Sn=1+2an,求通项公式an.
【答案】
分析:(1)利用公式
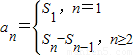
,由S
n=3
n+1,能求出a
n.
(2)由S
n=1+2a
n,解得a
1=-1.a
n=S
n-S
n-1=1+2a
n-1-2a
n-1,故a
n=2a
n-1,由此能求出数列{a
n}的通项公式a
n.
解答:解:(1)∵S
n=3
n+1,
∴a
1=S
1=3+1=4,
a
n=S
n-S
n-1=3
n+1-3
n-1-1=3
n-3
n-1.
当n=1时,3
n-3
n-1=2≠a
1,
∴a
n=
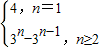
.
(2)∵S
n=1+2a
n,
∴当n=1时,a
1=1+2a
1,解得a
1=-1.
当n≥2时,S
n-1=1+2a
n-1,
∴a
n=S
n-S
n-1=1+2a
n-1-2a
n-1,
整理,得a
n=2a
n-1,
∴数列{a
n}是首项为-1,公比为2的等比数列,
∴a
n=-2
n-1.
点评:本题考查数列的通项公式的求法,解题时要认真审题,仔细解答,注意公式
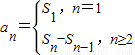
的灵活运用.

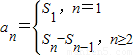 ,由Sn=3n+1,能求出an.
,由Sn=3n+1,能求出an.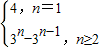 .
.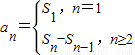 的灵活运用.
的灵活运用. 

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案