解:(1)f′(x)=x
2-(a+1)x+a=(x-1)(x-a)
当a>1时,函数f(x)在(-∞,1)及(a,a+1)上单调递增,在(1,a)上单调递减,
f(a+1)=-

+(a+1)a=

,
解不等式f(a)>0,得1<a<3,解不等式f(a+1)>0,得

函数f(x)在区间[0,a+1]的零点,当1<a<3时只有一个;当a=3时有两个;当3

时有三个零点,当a

时有两个零点.
(2)令h(x)=g(x)-e
x,z则h(0)=g(0)-1=a-1<0
我们只需证明h(x)在[0,+∞)上单调递减.
令t(x)=h′(x)=2x-(a+1)-e
x,则t′(x)=2-e
x,令2-e
x=0得x=ln2.
∴t(x)的最大值是t(ln2)=2ln2-(a+1)-e
ln2=2ln2-(a+1)-2<2ln2-2<0
∴t(x)<0在[0,+∞)上恒成立
∴g(x)-e
x在(0,+∞)上单调递减,g(x)<e
x在[0,+∞)上恒成立.
分析:(1)先求出导数f′(x)=x
2-(a+1)x+a=(x-1)(x-a),得到:当a>1时,函数f(x)在(-∞,1)及(a,a+1)上单调递增,在(1,a)上单调递减,由于f(0)=0,求出f(a+1)解不等式f(a)>0,得1<a<3,解不等式f(a+1)>0,得

,从而得出函数f(x)在区间[0,a+1]内零点的个数;
(2)令h(x)=g(x)-e
x,z则h(0)=g(0)-1=a-1<0,下面我们只需证明h(x)在[0,+∞)上单调递减.
令t(x)=h′(x)=2x-(a+1)-e
x,求出其导数,先研究t(x)的单调性,再利用导数求解t(x)在R上的最大值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值即得.
点评:本题考查的知识点是函数零点的判定定理,函数恒成立问题,利用导数求闭区间上的函数最值,(1)中根据已知条件构造构造关于b的不等式组是证明的关键;(2)中将不等式f(x)≤g(x)在
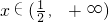
恒成立,转化为函数恒成立问题是解答的关键.

 x3-
x3- (a+1)x2+ax,g(x)=f′(x)是函数f(x)的导函数,其中实数a是不等1的常数.
(a+1)x2+ax,g(x)=f′(x)是函数f(x)的导函数,其中实数a是不等1的常数. +(a+1)a=
+(a+1)a= ,
,
 时有三个零点,当a
时有三个零点,当a 时有两个零点.
时有两个零点. ,从而得出函数f(x)在区间[0,a+1]内零点的个数;
,从而得出函数f(x)在区间[0,a+1]内零点的个数;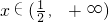 恒成立,转化为函数恒成立问题是解答的关键.
恒成立,转化为函数恒成立问题是解答的关键. 

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<