
思路解析:本题考查相互独立事件同时发生的概率的计算方法及分析、解决问题的能力.
解:设事件A1表示从甲箱子里摸出白球,事件A2表示从乙箱子里摸出白球,因为从甲箱子里摸球的结果不会影响从乙箱子里摸球的结果,所以A1和A2是相互独立的.
P(获胜)=P(A![]() =0.3.
=0.3.
误区警示 有人认为,两个箱子里装的白球比黑球多,所以获奖的概率大于0.5.你认为呢?
尽管两个箱子里装的白球比黑球多,但获奖的概率小于0.5.原因是除了两个球全是白球外,还有可能两个球全为黑球或两个球中一个为白球另一个为黑球.两个球全为黑球的概率为![]() ,两个球中一个为白球另一个为黑球的概率为1-0.3-0.2=0.5,所以由两个箱子里装的白球比黑球多只能推出摸出的两个球全为白球的概率大于摸出的两个球全为黑球的概率,但这两个事件的并不等于必然事件,所以不能推出获奖的概率大于0.5.
,两个球中一个为白球另一个为黑球的概率为1-0.3-0.2=0.5,所以由两个箱子里装的白球比黑球多只能推出摸出的两个球全为白球的概率大于摸出的两个球全为黑球的概率,但这两个事件的并不等于必然事件,所以不能推出获奖的概率大于0.5.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年四川省高三9月月考理科数学试卷(解析版) 题型:解答题
学校游园活动有这样一个游戏节目,甲箱子里装有3个白球、2个黑球;乙箱子里装有
1个白球、2个黑球。这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中:
①摸出3个白球的概率;
②获奖的概率;
(Ⅱ)求在两次游戏中获奖次数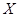 的分布列及数学期望
的分布列及数学期望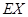 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同。每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率。
(2)求在两次游戏中获奖次数X的分布列及数学期望E(x)。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三下学期二调考试理科数学试卷(解析版) 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同。每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率。
(2)求在两次游戏中获奖次数X的分布列及数学期望E(x)。
【解析】(1) ①摸出3个白球,只有甲箱摸2个白球,乙箱摸一个白球;②不少于2个包括2个白球或3个白球。(2)符合几何分别。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com