设关于x的不等式ax2+bx+c>0的解集为{x|α<x<β,α>0}用α、β表示关于x的不等式cx2-bx+a>0的解集.
分析:由不等式ax2+bx+c>0的解集为{x|α<x<β,α>0}我们易得a>0,c>0,我们易给出不等式cx2-bx+a>0的解集的形式,结合韦达定理,我们求出方程cx2-bx+a=0的两个根,即可得到不等式cx2-bx+a>0的解集
解答:解:∵关于x的不等式ax
2+bx+c>0的解集为{x|α<x<β,α>0}
我们易得α+β=
->0,α•β=
>0,
且a,c同号,则a>0,c>0
则b=-a(α+β),c=a(α•β),
设m,n为不等式cx
2-bx+a>0的解集.
则m+n=
=-
=(-
)+(
-)
m•n=
=
=(-
)•(
-)
即-
,
-为方程cx
2-bx+a=0的两个根
又由0<α<β,
∴-
<
-故不等式cx
2-bx+a>0的解集为(-∞,-
)∪(
-,+∞)
点评:本题考查的知识点是一元二次不等式的应用,三个二次之间的辩证关系,其中根据x的不等式ax2+bx+c>0的解集为{x|α<x<β,α>0}判断a>0,c>0,进而确定不等式cx2-bx+a>0的解集的形式是解答本题的关键.



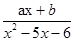 >0的解集为________.
>0的解集为________.