
求下列函数的单调区间.
(1)y=cos 2x;(2) .
.
|
解: (1)函数y=cos x的单调递增区间、单调递减区间分别由下面不等式确定:2kp -p ≤2x≤2kp (kÎ Z), 2kp ≤2x≤2kp +p (kÎ Z), ∴
∴函数 y=cos 2x的单调增区间、单调减区间分别为
(2) ∵ y=sin u(uÎ R)的递增、递减区间分别为
∴函数  的递增、递减区间分别由下列不等式确定. 的递增、递减区间分别由下列不等式确定.
得 
∴函数  的单调递增区间、单调递减区间分别为 的单调递增区间、单调递减区间分别为
可依据 y=sin x(xÎ R)和y=cos x(xÎ R)的单调区间来求. |
|
求形如 y=Asin(w x+φ)或y=Acos(w x+φ)(其中A≠0,w >0的函数的单调区间,可以通过解不等式的方法去解答,列不等式的原则是:①把“w x+φ(w >0)”视为一个“整体”;②A>0(A<0)时,所列不等式的方向与y=sin x(xÎ R);y=cos x(xÎ R)的单调区间对应的不等式方向相同(反). |


科目:高中数学 来源:2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷(四)(解析版) 题型:解答题
求下列函数的单调区间:
(1)y=tan ; (2)y=
; (2)y= tan2x+1;
tan2x+1;
(3)y=3tan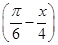 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com