
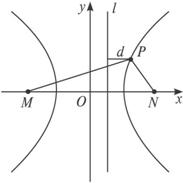
(1)求点P的轨迹方程;
(2)设d为点P到直线l:x=![]() 的距离,若|PM|=2|PN|2,求
的距离,若|PM|=2|PN|2,求![]() 的值.
的值.
(1)解:由双曲线的定义,点P的轨迹是以M、N为焦点,实轴长2a=2的双曲线,因此半焦距c=2,实半轴a=1,从而虚半轴b=![]() .
.
所以双曲线的方程为x2![]() =1.
=1.
(2)解法一:由(1)及图(1),易知|PN|≥1,因|PM|=2|PN|2, ①

(1)?
知|PM|>|PN|,故P为双曲线右支上的点,所以|PM|=|PN|+2. ②
将②代入①,得2|PN|2-|PN|-2=0,解得|PN|=![]() ,舍去
,舍去![]() ,所以|PN|=
,所以|PN|=![]() .
.
因为双曲线的离心率e=![]() =2,直线l:x=
=2,直线l:x=![]() 是双曲线的右准线,故
是双曲线的右准线,故![]() =e=2,所以d=
=e=2,所以d=![]() |PN|,
|PN|,
因此![]() =
=![]() =
=![]() =4|PN|=1+
=4|PN|=1+![]() .
.
解法二:设P(x,y).因|PN|≥1知|PM|=2|PN|2≥2|PN|>|PN|,故P在双曲线右支上,所以x≥1.由双曲线方程有y2=3x2-3,
因此|PM|=![]() =
=![]() =
=![]() =2x+1.
=2x+1.
|PN|=![]() =
=![]() =
=![]() .
.
从而由|PM|=2|PN|2得2x+1=2(4x2-4x+1),即8x2-10x+1=0.
所以x=![]() (舍去x=
(舍去x=![]() ).
).
有|PM|=2x+1=![]() ,d=x-
,d=x-![]() =
=![]() .
.
故![]() =
=![]() ·
·![]() =1+
=1+![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
| 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| 48 |
| x |
| b |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 2 |

| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
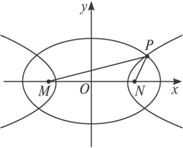
(1)求点P的轨迹方程;
(2)若|PM|·|PN|=![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com