
 -
- +cos2x)对一切实数x均成立,则实数m的范围________.
+cos2x)对一切实数x均成立,则实数m的范围________. ≤m≤3或m=-
≤m≤3或m=-
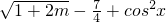 ≤4…②,
≤4…②, ;
; -
- +cos2x)对一切实数x均成立,
+cos2x)对一切实数x均成立,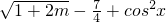 …③,(m≥-
…③,(m≥- )
)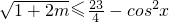 ,∴
,∴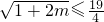 ,解得m≤
,解得m≤ ,
, +
+ ≥-sin2x-sinx=-(sinx+
≥-sin2x-sinx=-(sinx+ )2+
)2+ ,
, )2≥
)2≥ -m-
-m- ,∵-1≤sinx≤1,
,∵-1≤sinx≤1, 时(sinx+
时(sinx+ )2取最小值为0,
)2取最小值为0, -m-
-m- ,解得m≥
,解得m≥ 或m=-
或m=- ,
, ≤m≤3或m=-
≤m≤3或m=- ;
; ≤m≤3或m=-
≤m≤3或m=-


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A.[2,5] B.[1,+∞]
C.[2,10] D.[2,13 ]
查看答案和解析>>
科目:高中数学 来源:2010年山西省太原二中高考数学二模试卷(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省南充市高三适应性考试数学理卷 题型:选择题
定义在区间[2,4]上的函数 (m是实常数)的图象过点(2,1),则函数
(m是实常数)的图象过点(2,1),则函数 的值域为 ( )
的值域为 ( )
A.[2,5] B. C.[2,10] D.[2,13]
C.[2,10] D.[2,13]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com