练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1)设f(x)＝

    (2)求

    答案：
    解析：

    　　解：(1)

    　　

    　　(2)由

    　　

    　　绿色通道：(1)分段函数在区间[a，b]上的积分可分成几段积分的和的形式．

    　　(2)分段的标准是使每一段上的函数表达式确定，按照原函数分段的情况分即可，无需分得过细．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东济宁金乡一中2011-2012学年高一上学期12月月考数学试题 题型：044

    设函数f(x)＝loga(1－x)，g(x)＝loga(1＋x)(a＞0且a≠1)．

    (1)设F(x)＝f(x)－g(x)，判断F(x)的奇偶性并证明；

    (2)若关于x的方程有两个不等实根，求实数m的范围；

    (3)若a＞1且在x∈[0，1]时，恒成立，求实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源：山东省鱼台二中2011-2012学年高一上学期期末模拟考试数学试题 题型：044

    设函数，(a＞0且a≠1)．

    (1)设F(x)＝f(x)－g(x)，判断F(x)的奇偶性并证明；

    (2)若关于x的方程有两个不等实根，求实数m的范围；

    (3)若a＞1且在x∈[0，1]时，恒成立，求实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分12分）已知＝(cos＋sin，－sin)，＝(cos－sin，2cos).

     (1)设f(x)＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈，且f(x1)＝f(x2)＝1，求x1＋x2的值.

    查看答案和解析>>

    科目：高中数学 来源：2014届河北衡水中学高一第二学期期末文科数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    已知＝(cos＋sin，－sin)，＝(cos－sin，2cos).

    (1)设f(x)＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈，且f(x1)＝f(x2)＝1，求x1＋x2的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届湖北长阳自治县第一中学高二下学期期中理科数学试卷（解析版） 题型：解答题

    已知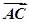＝(cos＋sin，－sin)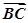，＝(cos－sin，2cos).

    (1)设f(x)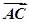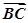＝·，求f(x)的最小正周期和单调递减区间；

    (2)设有不相等的两个实数x1，x2∈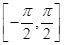，且f(x1)＝f(x2)＝1，求x1＋x2的值.

     

    查看答案和解析>>

    同步练习册答案