
函数f(x)=ln x-![]() 零点所在的大致区间是
零点所在的大致区间是
A.(1,2)
B.(2,3)
C.(1,![]() )和(3,4)
)和(3,4)
D.(e,+∞)
|
解析:用验证法.从已知的区间(a,b)求f(a)、f(b),判断是否有f(a)·(b)<0.∵f(1)=-2<0,f(2)=ln 2-1<0,∴在(1,2)内f(x)无零点,故排除A.∵f(3)= ln 3- |
|
确定零点所在区间,只要判断区间[a,b]的端点值的乘积是否有f(a)f·(b)<0,并且看函数y=f(x)在[a,b]上是否是连续曲线.这里说“若f(a)·f(b)<0,则在区间(a,b)内方程f(x)=0至少有一个实数解”,指出了方程f(x)=0实数解的存在,并不能判断具体有多少个实数解. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
设g(x)是函数f(x)=ln(x+1)+2x的导函数,若函数g(x)按向量a平移后得到函数y=![]() ,则向量a等于
,则向量a等于
A.(1,2) B.(-1,-2) C.(-2,-1) D.(2,1)
查看答案和解析>>
科目:高中数学 来源:2010年湖南省洞口四中下学期高二单元数学试题 题型:解答题
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若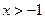 ,证明:
,证明: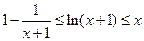 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古高三下学期综合检测(一)文科数学试卷(解析版) 题型:选择题
函数f(x)=ln(4+3x-x2)的单调递减区间是
A.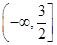 B.
B.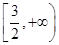 C.
C.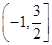 D.
D.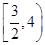
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省高二下学期期末考试理科数学卷 题型:选择题
已知函数f(x)=ln(x+1)- x2+x-m(m为常数)的图象上P点处的切线与直线x-
x2+x-m(m为常数)的图象上P点处的切线与直线x- y+2=0的夹角为45°,则点P的横坐标为(
)
y+2=0的夹角为45°,则点P的横坐标为(
)
A.
0 B.  C.
C.  D. ±
D. ±
查看答案和解析>>
科目:高中数学 来源:2010年湖南省下学期高二单元数学试题 题型:解答题
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若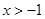 ,证明:
,证明: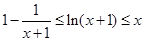 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com