
分析 (1)消去y,得到关于x的不等式,求出x的范围即可;(2)根据基本不等式的性质证明即可.
解答 解:(1)∵2x+y=9,
∴由|8-y|<x+3,得|2x-1|<x+3,
则-x-3<2x-1<x+3,
即$\left\{\begin{array}{l}{2x-1<x+3}\\{2x-1>-x-3}\end{array}\right.$,
解得:-$\frac{2}{3}$<x<4;
(2)证明:∵2x+y=9,x>0,y>0,
∴$\frac{x+8y}{2xy}$=$\frac{4}{x}$+$\frac{1}{2y}$=$\frac{1}{9}$(2x+y)($\frac{4}{x}$+$\frac{1}{2y}$)=$\frac{1}{9}$[$\frac{17}{2}$+($\frac{4y}{x}$+$\frac{x}{y}$)],
∵$\frac{4y}{x}$+$\frac{x}{y}$≥4,当且仅当x=2y=$\frac{18}{5}$时“=”成立,
∴$\frac{x+8y}{2xy}$≥$\frac{1}{9}$×($\frac{17}{2}$+4)=$\frac{25}{18}$.
点评 本题考查了绝对值不等式问题,考查基本不等式的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )
某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )| A. | 甲城销售额多,乙城不够稳定 | B. | 甲城销售额多,乙城稳定 | ||
| C. | 乙城销售额多,甲城稳定 | D. | 乙城销售额多,甲城不够稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 21 | D. | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组| A. | 32 | B. | 40 | C. | 48 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7<a<24 | B. | -24<a<7 | C. | a<-1或a>24 | D. | a<-24或a>7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
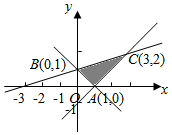 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | ab<b2 | C. | ab>a2 | D. | $a-\frac{1}{a}<b-\frac{1}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com