
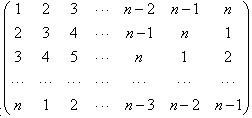 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99=________.
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99=________. 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:2010年普通高等学校招生全国统一考试、理科数学(上海卷) 题型:022
在n行n列矩阵 中,记位于第i行第j列的数为aij(i,j=1,2,…,n).当n=9时,a11+a22+a33+…+a99=________.
中,记位于第i行第j列的数为aij(i,j=1,2,…,n).当n=9时,a11+a22+a33+…+a99=________.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:排列组合与二项式定理(解析版) 题型:解答题
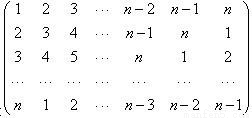 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .查看答案和解析>>
科目:高中数学 来源:2010年高考数学试卷精编:15.6 积分、行列式及矩阵(解析版) 题型:解答题
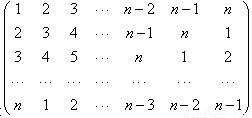 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com