Question

已知函数f（x）是以1为周期的偶函数，且当x∈（0，1）时，f（x）=2^x，则f（-log₂3）的值为________．

Answer 1

分析：先判断log₂3的范围，利用函数的周期为1转化到区间（0，1）内，再根据偶函数的定义和对数的运算性质求出f（log₂3）的值．
解答：∵1＜log₂3＜2，∴0＜log₂3-1＜1．
∵函数f（x）是以1为周期的偶函数，
∴f（-log₂3）=f（log₂3）=f（log₂3-1）=f（）．
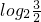
∵当x∈（0，1）时，f（x）=2^x ，
∴f（-log₂3）=f（）==，
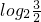
故答案为 ．
点评：本题考查了函数奇偶性和周期性的应用，根据周期性把自变量的范围转化到与题意有关的区间上，再由奇偶性联系f（x）=f（-x），利用对数的运算性质求出函数值．