已知定义在R上的函数y=f(x)满足:对?x,y∈R,都有f(x+y)=f(x)+f(y)-3,并且当x>0时,f(x)<3.
(1)求f(0)的值;
(2)判断f(x)是R上的单调性并作出证明;
(3)若不等式f((t-2)|x-4|)+3>f(t2+8)+f(5-4t)对t∈(2,4)恒成立,求实数x的取值范围.
解:(1)令x=0,y=0,则f(0+0)=f(0)+f(0)-3,
∴f(0)=3;
(2)f(x)是R上的减函数,证明如下:
设x
1>x
2,f(x
1)-f(x
2)=f(x
1-x
2+x
2)-f(x
2)=f(x
1-x
2)+f(x
2)-3-f(x
2)=f(x
1-x
2)-3,
∵x
1-x
2>0,
∴f(x
1-x
2)<3,
∴f(x
1)<f(x
2),即f(x)是R上的减函数;
(3)由(2)知f(x)是R上的减函数,
∴(t-2)|x-4|<t
2-4t+13对t∈(2,4)恒成立,
∴
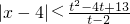
对t∈(2,4)恒成立,
∴|x-4|<
∴
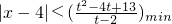
设
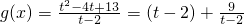
,当t∈(2,4)时
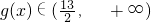
于是
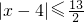
,解得:
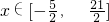
.
分析:(1)利用赋值法,令x=0,y=0,结合f(x+y)=f(x)+f(y)-3,可求f(0)的值;
(2)在R上设出两个变量,利用当x>0时,f(x)<3,确定函数值的大小关系,即可证得结论;
(3)利用单调性,转化为具体不等式,再分离参数,利用基本不等式,即可求得实数x的取值范围.
点评:本题考查抽象函数,考查赋值法的运用,考查函数单调性的证明,考查恒成立问题,考查分离参数、基本不等式的运用,正确分离参数,求出最值是关键.

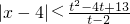 对t∈(2,4)恒成立,
对t∈(2,4)恒成立,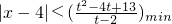
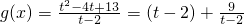 ,当t∈(2,4)时
,当t∈(2,4)时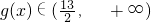
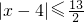 ,解得:
,解得: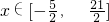 .
.
