练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    △ABC 的内心为I，三角形内一点P 满足 ∠PBA+∠PCA=∠PBC+∠PCB．求证， AP≥AI，而且等号当且仅当P=I 时成立．

    证明：∠PBC+∠PCB= (∠ABC+∠ACB)=∠IBC+∠ICB，故∠PBI=∠PCI，从而

    P，B，C，I 四点共圆．但由内外角平分线相垂直知 B，C，I 与 BC 边上的旁切圆心T 共圆，且IT 是这个圆的直径，IT 的中点O为圆心．由于A，I，T 共线(∠BAC 的平分线)，且 P在圆周上，AP+PO≥AO=AI+IO ， PO=IO，故AP≥AI．

    等号当且仅当P 为线段AO与圆周的交点即P=I 时成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练12练习卷（解析版） 题型：解答题

    如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.

    (1)求证A,I,H,E四点共圆;

    (2)若∠C=50°,求∠IEH的度数.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南郑州高三第一次质量预测理数学试卷（解析版） 题型：解答题

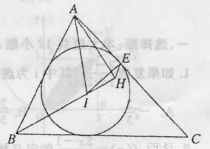
    选修4—1：几何证明选讲如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.

    （Ⅰ）求证：四点Ａ，Ｉ，Ｈ，Ｅ共圆；

    （Ⅱ）若∠C=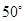，求∠IEH的度数.

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南郑州高三第一次质量预测文科数学试卷（解析版） 题型：解答题

    选修4—1：几何证明选讲

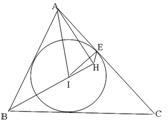
    如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.

    （Ⅰ）求证：四点Ａ，Ｉ，Ｈ，Ｅ共圆；

    （Ⅱ）若∠C=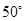，求∠IEH的度数.

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省镇平一高高三下学期第四次周考文科数学试卷 题型：解答题

    (本小题满分10分)选修4－1：几何证明选讲

    如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.

    (Ⅰ)求证：四点A，I，H，E共圆；

    (Ⅱ)若∠C＝50°，求∠IEH的度数.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省郑州市高三第一次质量预测理科数学试卷 题型：解答题

    如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.

    （Ⅰ）求证：四点Ａ，Ｉ，Ｈ，Ｅ共圆；

    （Ⅱ）若∠C=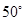，求∠IEH的度数.

     

    查看答案和解析>>

    同步练习册答案