练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数在上具有单调性,则实数的取值范围是         

           

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：广东省梅县东山中学2012届高三上学期期中考试数学文科试题 题型：044

    设f(x)是定义在区间(1，＋∞)上的函数，其导函数为(x)．如果存在实数a和函数h(x)，其中h(x)对任意的x∈(1，＋∞)都有h(x)＞0，使得(x)＝h(x)(x2－ax＋1)，则称函数f(x)具有性质P(a)．

    (1)设函数f(x)＝lnx＋(x＞1)，其中b为实数

    (ⅰ)求证：函数f(x)具有性质P(b)

    (ⅱ)求函数f(x)的单调区间；

    (2)已知函数g(x)具有性质P(2)，给定x1，x2∈(1，＋∞)，x1＜x2，设m为实数，α＝mx1＋(1－m)x2，β＝(1－m)x1＋mx2，且α＞1，β＞1，若|g(α)－g(β)|＜|g(x1)－g(x2)|，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年黑龙江省高一期中考试数学卷 题型：解答题

    已知函数．

    （1）证明函数具有奇偶性；

    （2）证明函数在上是单调函数；

    （3）求函数在上的最值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知k∈R，函数f（x）=ax+k•bx（a＞0，且a≠1；b＞0，且b≠1）
    （1）已知函数数学公式在区间（0，1]上单调递减，在区间[1，+∞）上单调递增．若数学公式，求函数f（x）的单调区间．
    （2）若实数a，b满足ab=1．求k的值，使得函数f（x）具有奇偶性．（写出完整解题过程）

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年浙江省衢州市衢江区杜泽中学高一（上）第二次段考数学试卷（解析版） 题型：解答题

    已知k∈R，函数f（x）=ax+k•bx（a＞0，且a≠1；b＞0，且b≠1）
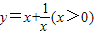    （1）已知函数在区间（0，1]上单调递减，在区间[1，+∞）上单调递增．若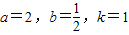，求函数f（x）的单调区间．
    （2）若实数a，b满足ab=1．求k的值，使得函数f（x）具有奇偶性．（写出完整解题过程）

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省大庆铁人中学2010-2011学年高三第二次月考 题型：解答题

     已知函数．

       （1）证明函数具有奇偶性；

       （2）证明函数在上是单调函数；

       （3）求函数在上的最值．

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案