
分析 求出圆心和半径.设过该点的直线方程,求圆心到直线的距离与半径和半弦长构成勾股定理,解出斜率k,即得到直线方程.
解答 解:∵圆C:x2+y2+4x-12y+24=0,其圆心坐标为(-2,6),半径为r=4,点P(0,5),
设过P的直线方程为:y=kx+5,化为一般方程:kx-y+5=0
圆心到直线的距离d=$\frac{|Ax+By+C|}{\sqrt{{A}^{2}+{B}^{2}}}$.
∴d=$\frac{|-2k-6+5|}{\sqrt{1+{k}^{2}}}$
∴$(2{\sqrt{3})^{2}+d}^{2}={r}^{2}$,
解得:k=$\frac{3}{4}$,
所以3x-4y+20=0,
又因为过某一点可以做两条直线截得的弦长相等,而k只有一个值,那么另一个k值不存在,又要过P,
所以:直线方程为:x=0,
故填:3x-4y+20=0或x=0.
点评 本题考查了弦长问题.过某一点截得的弦长问题:如果弦长等于直径,直线过圆心.否则必有两条直线截得的弦长相等,设过该点的直线方程,求圆心到直线的距离与半径和半弦长构成勾股定理,解出斜率k,如果k只有一个值,那么另一个k值不存在,直线与y轴平行.属于基础题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{32}$,0) | B. | (-$\frac{1}{16}$,0) | C. | (0,$\frac{1}{32}$) | D. | (0,$\frac{1}{16}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3∈A | B. | A=B | C. | A∩B=A | D. | A∪B=Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
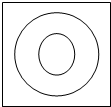 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:
如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{7}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生510天.
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生510天.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com