练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的以O为圆心的转盘一次，并获得相应金额的返券，假定指针等可能地指向任一位置(不指向各区域的边界)．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

    (Ⅰ)若某位顾客消费128元，求返券金额不低于30元的概率；

    (Ⅱ)若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X(元)．求随机变量X的分布列和数学期望．

    答案：
    解析：

    　　解：(Ⅰ)设指针落在A，B，C区域分别记为事件A，B，C．

    　　则　3分

    　　若返券金额不低于30元，则指针落在A或B区域．

    　　　5分

    　　即消费128元的顾客，返券金额不低于30元的概率是．

    　　(Ⅱ)由题意得，该顾客可转动转盘2次．

    　　随机变量的可能值为0，30，60，90，120．　6分

    　　

    　　9分

    　　所以，随机变量的分布列为：

    　　其数学期望

    　　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

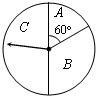    精英家教网某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
    （Ⅰ）若某位顾客消费128元，求返券金额不低于30元的概率；
    （Ⅱ）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X（元）．求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

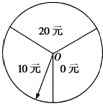    精英家教网某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费每满100元可以转动如图所示的圆盘一次，其中O为圆心，且标有20元、10元、0元的三部分区域面积相等．假定指针停在任一位置都是等可能的．当指针停在某区域时，返相应金额的优惠券．（例如：某顾客消费了218元，第一次转动获得了20元，第二次获得了10元，则其共获得了30元优惠券．）顾客甲和乙都到商场进行了消费，并按照规则参与了活动．
    （Ⅰ）若顾客甲消费了128元，求他获得优惠券面额大于0元的概率？
    （Ⅱ）若顾客乙消费了280元，求他总共获得优惠券金额不低于20元的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    指针位置 A区域 B区域 C区域
    返存金额（单位：元） 60 30 0
    五一节期间，某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如
    图所示的转盘一次，并获得相应金额的返券．（假定指针等可能地停在任一位置，指针落在区域的边界时，重新转一次）指针所在的区域及对应的返劵金额见右上表．
    例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
    （1）已知顾客甲消费后获得n次转动转盘的机会，已知他每转一次转盘指针落在区域边界的概率为p，每次转动转盘的结果相互独立，设ξ为顾客甲转动转盘指针落在区域边界的次数，ξ的数学期望Eξ=
    1
    25
    ，标准差σξ=
    3
    		11
    50
    ，求n、p的值；
    （2）顾客乙消费280元，并按规则参与了活动，他获得返券的金额记为η（元）．求随机变量η的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某商场为吸引顾客消费推出一项促销活动，促销规则如下：到该商场购物消费满100元就可转动如图所示的转盘一次，进行抽奖（转盘为十二等分的圆盘），满200元转两次，以此类推；在转动过程中，假定指针停在转盘的任一位置都是等可能的，若转盘的指针落在A区域，则顾客中一等奖，获得10元奖金，若转盘落在B区域或C区域，则顾客中二等奖，获得5元奖金；若转盘指针落在其它区域则不中奖（若指针停到两区间的实线处，则重新转动）．若顾客在一次消费中多次中奖，则对其奖励进行累加．已知顾客甲到该商场购物消费了268元，并按照规则能与了促销活动．
    （Ⅰ） 求顾客甲中一等奖的概率；
    （Ⅱ） 记ξ为顾客甲所得的奖金数，求ξ的分布列及其数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题满分13分)

        某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

      （I）若某位顾客消费128元，求返券金额不低于30元的概率；

      （II）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X(元)．

        求随机变量X的分布列和数学期望。

    查看答案和解析>>

    同步练习册答案