解:(1)设 B(-2

,0)…(1分)
则|

+

|+|

-

|=|

+

|+|

-

|=|

|+|

|=6
∴M 的轨迹为以 A、B 为焦点,长轴长为 6 的椭圆
由c=2

,2a=6?a=3?b=1 …(5分)
∴M 的轨迹 C的方程为

+y
2=1 …(6分)
(2)设直线 l 的方程为 y=kx+2(k≠0且k存在),…(7分)
由
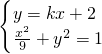
得x
2+9 (kx+2)
2=9,
即 (1+9k
2) x
2+36kx+27=0 …(8分)
∴△=(36k)
2-4×27 (1+9k
2)>0
即 9k
2-3>0,∴k<-

或k>

(*)…(9分)
设P(x
1,y
1),Q(x
2,y
2)
∴x
1+x
2=-
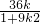
,x
1x
2=
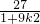
…(10分)
∵以 PQ 为直径的圆过原点,
∴x
1x
2+y
1y
2=0,即x
1x
2+(kx
1+2)(kx
2+2)=0
∴(1+k
2) x
1 x
2+2k (x
1+x
2)+4=0
即
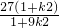
-
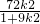
+4=0
解得k=±

满足 (*)
∴满足条件的直线 l 存在,
且直线 l 的方程为:
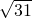
x-3y+6=0或
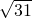
x+3y-6=0 …(12分)
分析:(1)设 B(-2

,0),则|

+

|+|

-

|=|

+

|+|

-

|=|

|+|

|=6,所以M 的轨迹为以 A、B 为焦点,长轴长为6的椭圆,由此能求出M的轨迹C的方程.
(2)设直线 l 的方程为 y=kx+2,由
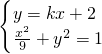
得(1+9k
2) x
2+36kx+27=0,再由根的判别式和韦达定理进行求解.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

 =(2
=(2 ,0),O是坐标原点,动点 M 满足:|
,0),O是坐标原点,动点 M 满足:| +
+ |+|
|+| -
- |=6.
|=6. ,0)…(1分)
,0)…(1分) +
+ |+|
|+| -
- |=|
|=| +
+ |+|
|+| -
- |=|
|=| |+|
|+| |=6
|=6 ,2a=6?a=3?b=1 …(5分)
,2a=6?a=3?b=1 …(5分) +y2=1 …(6分)
+y2=1 …(6分)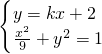 得x2+9 (kx+2)2=9,
得x2+9 (kx+2)2=9, 或k>
或k> (*)…(9分)
(*)…(9分)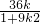 ,x1x2=
,x1x2=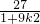 …(10分)
…(10分)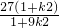 -
-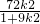 +4=0
+4=0 满足 (*)
满足 (*)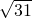 x-3y+6=0或
x-3y+6=0或 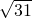 x+3y-6=0 …(12分)
x+3y-6=0 …(12分) ,0),则|
,0),则| +
+ |+|
|+| -
- |=|
|=| +
+ |+|
|+| -
- |=|
|=| |+|
|+| |=6,所以M 的轨迹为以 A、B 为焦点,长轴长为6的椭圆,由此能求出M的轨迹C的方程.
|=6,所以M 的轨迹为以 A、B 为焦点,长轴长为6的椭圆,由此能求出M的轨迹C的方程.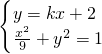 得(1+9k2) x2+36kx+27=0,再由根的判别式和韦达定理进行求解.
得(1+9k2) x2+36kx+27=0,再由根的判别式和韦达定理进行求解.
