练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知α∈(0,π),求证:2sin2α≤.

    证法一:(分析法)?

    要证明2sin2α≤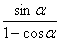成立,?

    只要证明4sinαcosα≤.?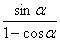

    ∵α∈(0,π),∴sinα＞0.?

    只要证明4cosα≤.?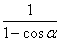

    上式可变形为4≤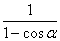+4(1-cosα).?

    ∵1-cosα＞0,?

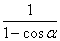    ∴+4(1-cosα)≥2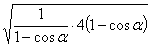=4,?

    当且仅当cos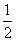α=,即α=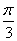时取等号.?

    ∴4≤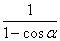+4(1-cosα)成立.?

    ∴不等式2sin2α≤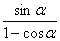成立.

    证法二:(综合法)?

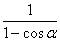    ∵+4(1-cosα)≥4,?

    (1-cosα＞0,当且仅当cos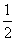α=即α=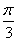时取等号)?

    ∴4cosα≤.?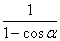

    ∵α∈(0,π),?∴sinα＞0.?

    ∴4sinαcosα≤.?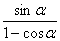

    ∴2sin2α≤.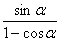

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知0＜x＜
    43
    ，求x（4-3x）的最大值
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0＜α＜
    π
    4
    ，设x=（sinα）sinα，y=（cosα）sinα，z=（sinα）cosα，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0＜θ＜1800，且θ角的6倍角的终边和θ角终边重合，则满足条件的角θ为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0＜m＜n＜1，则a=logm（m+1）
    ＞
    ＞
    b=logn（n+1）（在横线上填“＞”，“＜”或“=”）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0＜x＜1，则函数y=
    1
    x
    +
    4
    1-x
    的最小值是
     
    ．

    查看答案和解析>>

    同步练习册答案