Question

如图，在正方体ABCD—A₁B₁C₁D₁中，E为AB的中点.

（1）求异面直线A₁E与BD₁所成角的余弦值；

（2）求二面角A₁-EC-A的大小.

 

Answer 1

解：（1）设正方体的棱长为1，延长DC至G，使CG=DC,连结BG、D₁G，∵CEB，∴四边形EBGC是平行四边形.

∴BG∥EC.∴∠D₁BG是异面直线BD₁与CE所成的角.

在△D₁BG中D₁B=，BG=，D₁G=，

∴cosD₁BG=，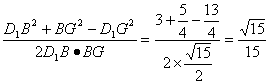

即异面直线A₁H⊥CE与CE所成角的余弦值是.

（2）过A₁作A₁H⊥CE交CE的延长线于H.连结AH.

∵AA₁⊥平面ABCD，∴AH是A₁H在平面ABCD内的射影.∴AH⊥CH.

则∠A₁HA为二面角A₁-EC-D的平面角.

底面ABCD如图所示.

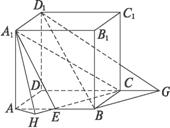
由于∠AHE=∠B=90°，∠AEH=∠CEB，则△AHE∽△CBE.

∴，∴CE=，AE=，∴AH=。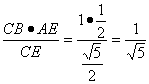

在Rt△A₁AH中，A₁A=1，AH=，∴tanA₁HA=.

则二面角A₁-EC-D角的大小为arctan.