
一个盒子装有六张卡片,上面分别写着如下六个定义域为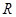 的函数:
的函数: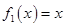 ,
,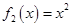 ,
,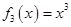 ,
,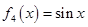 ,
,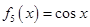 ,
,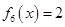 .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数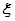 的分布列和数学期望.
的分布列和数学期望.
(1)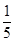 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)利用性质“奇函数+奇函数=奇函数”这一性质得到所抽取的两个函数都是奇函数,然后再用排列组合结合古典概型的概率公式计算相应事件的概率;(2)先列举出随机变量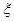 的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.
的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.
试题解析:(1)六个函数中是奇函数的有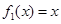 ,
,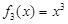 ,
,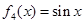 ,
,
由这3个奇函数中的任意两个函数相加均可得一个新的奇函数.
记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,
由题意知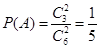 ;
;
(2)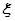 可取1,2,3,4 ,
可取1,2,3,4 ,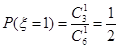 ,
, 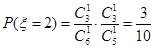
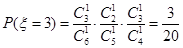 ,
,
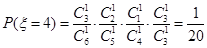 ,
,
故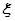 的分布列为
的分布列为
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
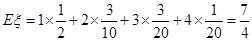
答: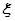 的数学期望为
的数学期望为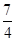 .
.
考点:1.排列组合;2.条件概率;3.随机变量的概率分布列与数学期望


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x-1 |
| 2x+1 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| x2+1 |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin2x+1 |
| 2x-1 |
| 2x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com