
 的单调增区间可能是
的单调增区间可能是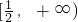


 ,
, ,注意到x<0或x>
,注意到x<0或x> ,
, ,+∞)上是增函数;
,+∞)上是增函数; ,+∞)上是减函数.
,+∞)上是减函数. 的单调增区间可能是(1,+∞).
的单调增区间可能是(1,+∞).

 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源:2012-2013学年广东省湛江二中高一(上)期中数学试卷(解析版) 题型:填空题
 的单调增区间是(-∞,1);
的单调增区间是(-∞,1); (x∈R)的值域为(-1,1);
(x∈R)的值域为(-1,1); .
.查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一年级期中考试数学试卷 题型:填空题
下列说法:
1、函数 的单调增区间是
的单调增区间是 ;
;
2、若函数 定义域为
定义域为 且满足
且满足 ,则它的图象关于
,则它的图象关于 轴对称;
轴对称;
3、函数 的值域为
的值域为 ;
;
4、函数 的图象和直线
的图象和直线 的公共点个数是
的公共点个数是 ,则
,则 的值可能是0,2,3,4;
的值可能是0,2,3,4;
5、若函数 在
在 上有零点,则实数
上有零点,则实数 的取值范围是
的取值范围是 .
.
其中正确的序号是 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com