(1)证明:由S
n+2-(t+1)S
n+1+tS
n=0,
得tS
n+1-tS
n=S
n+2-S
n+1,即a
n+2=ta
n+1(n∈N
*),
∴

,
又a
1=t(t≠0),a
2=t
2,∴

,
∴数列{a
n}是以t为首项,t为公比的等比数列,
∴a
n=t
n;
(2)解:∵(t
n+t
-n)-(2
n+2
-n)
=

=

=(t
n-2
n)[1-(
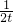
)
n].
又

<t<2,∴

<
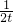
<1,
则t
n-2
n<0且1-(
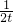
)
n>0,
∴(t
n-2
n)[1-(
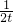
)
n]<0,
∴t
n+t
-n<2
n+2
-n.
(3)证明:∵

=

,
∴

=

(t
n+t
-n),
∴2(

+

+…+

)<(2+2
2+…2
n)+(2
-1+2
-2+…+2
-n)
=

=2(2
n-1)+1-2
-n=2
n+1-(1+2
-n)<2
n+1-2

,
∴

+

+…+

<2
n-

.
分析:(1)把给出的递推式展开后整理,得到a
n+2=ta
n+1,由给出的a
1=t(t≠0),即可说明数列{a
n}是等比数列,则通项公式可求;
(2)直接作差后由t的范围可得差式的符号,则给出的两个代数式的大小得到比较;
(3)把(1)中求出的a
n的通项公式代入,整理后可得

=

(t
n+t
-n),不等式右侧放缩后利用等比数列求和公式可得结论.
点评:本题考查了由递推式变形得数列的等比关系,考查了等比数列的通项公式,考查了作差法比较两个代数式的大小,(3)中的放缩证明不等式是该题的难点,此题属难题.

 <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小; <t<2,bn=
<t<2,bn=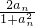 ,求证:
,求证: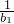 +
+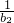 +…+
+…+ <2n-
<2n- .
. ,
, ,
,

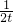 )n].
)n]. <t<2,∴
<t<2,∴ <
<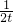 <1,
<1,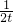 )n>0,
)n>0,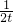 )n]<0,
)n]<0, =
= ,
, =
= (tn+t-n),
(tn+t-n), +
+ +…+
+…+ )<(2+22+…2n)+(2-1+2-2+…+2-n)
)<(2+22+…2n)+(2-1+2-2+…+2-n)
 ,
, +
+ +…+
+…+ <2n-
<2n- .
. =
= (tn+t-n),不等式右侧放缩后利用等比数列求和公式可得结论.
(tn+t-n),不等式右侧放缩后利用等比数列求和公式可得结论.
