练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f(x)=tanx,x∈(0,),若x1、x2∈(0,),且x1≠x2,求证：［f(x1)+f(x2)］＞f().

    分析:题目中条件与结论之间的关系不明显，因此可以用分析法挖掘本题中的隐含条件，在证明过程中要注意分析法的格式与步骤.

    证明：欲证［f(x1)+f(x2)］＞f(),

    即证（tanx1+tanx2）＞tan,

    只需证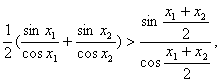

    即证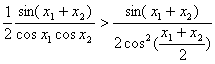

    ∵x1,x2∈(0,),∴x1+x2∈(0,π).

    ∴sin(x1+x2)＞0,1+cos(x1+x2)＞0,

    cosx1cosx2＞0.

    ∴只需证1+cos(x1+x2)＞2cosx1cosx2,

    即证cos(x1-x2)＜1.

    ∵x1,x2∈(0,),且x1≠x2,

    ∴cos(x1-x2)＜1显然成立.

    ∴原不等式成立.

    绿色通道:

    本题主要考查了三角函数与不等式证明的综合应用,在证明过程中注意角的取值范围及三角恒等变形公式的灵活运用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1-2x1+2x
    ．
    （1）试确定f（x）的奇偶性；
    （2）求证：函数f（x）在R上是减函数；
    （3）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    x3+2x2+5x+tex

    （1）当t=5时，求函数f（x）的单调区间；
    （2）若存在t∈[0，1]，使得对任意x∈[-4，m]，不等式f（x）≤x成立，求整数m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    a(x-1)2+1
    bx+c-b
    （a，b，c∈N），且f（2）=2，f（3）＜3，
    且f（x）的图象按向量
    e
    =(-1，0)    平移后得到的图象关于原点对称．
    （1）求a、b、c的值；
    （2）设0＜|x|＜1，0＜|t|≤1，求证不等式|t+x|-|t-x|＜|f（tx+1）|；
    （3）已知x＞0，n∈N*，求证不等式[f（x+1）]n-f（xn+1）≥2n-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•闵行区一模）已知函数f(x)=loga
    1-x1+x
    (0＜a＜1)    ．
    （1）求函数f（x）的定义域D，并判断f（x）的奇偶性；
    （2）如果当x∈（t，a）时，f（x）的值域是（-∞，1），求a与t的值；
    （3）对任意的x1，x2∈D，是否存在x3∈D，使得f（x1）+f（x2）=f（x3），若存在，求出x3；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=(t∈R)在［1,2］上的最小值为,P1(x1,y1),P2(x2,y2)是函数f(x)=图象上不同两点,且线段P1P2的中点P的横坐标为.

    (1)求t的值;

    (2)求证:点P的纵坐标是定值;

    (3)若数列{an}的通项公式为an=f()(m∈N*,n=1,2,…,m),求数列{an}的前m项和Sm.

    查看答案和解析>>

    同步练习册答案